دراسة خصائص الغاز المثالي موضوع مهم في الفيزياء. تبدأ مقدمة عن خصائص أنظمة الغاز بدراسة معادلة Boyle-Mariotte ، لأنها أول قانون تم اكتشافه تجريبيًا للغاز المثالي. دعونا ننظر في الأمر بمزيد من التفصيل في المقال.
ما هو المقصود بالغاز المثالي؟
قبل الحديث عن قانون Boyle-Mariotte والمعادلة التي تصفه ، دعنا نحدد الغاز المثالي. يُفهم عمومًا على أنه مادة سائلة لا تتفاعل فيها الجسيمات المكونة لها مع بعضها البعض ، وتكون أحجامها صغيرة بشكل مهم مقارنة بمتوسط المسافات بين الجسيمات.
في الواقع ، أي غاز حقيقي ، أي أن الذرات والجزيئات المكونة له لها حجم معين ولا تتفاعل مع بعضها البعض بمساعدة قوى فان دير فال. ومع ذلك ، عند درجات الحرارة العالية المطلقة (أكثر من 300 كلفن) والضغوط المنخفضة (أقل من جو واحد) ، تكون الطاقة الحركية للذرات والجزيئات أعلى بكثير من طاقة تفاعلات فان دير فال ، وبالتالي فإن الغاز الحقيقي عند المستوى المحدديمكن اعتبار الظروف ذات الدقة العالية مثالية.
معادلة بويل ماريوت
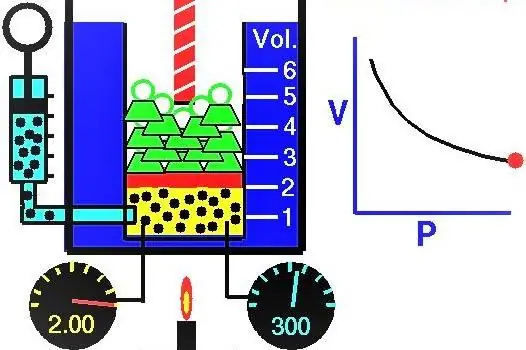
خصائص الغازات اكتشف العلماء الأوروبيون بنشاط خلال القرنين السابع عشر والتاسع عشر. كان أول قانون للغاز تم اكتشافه تجريبياً هو القانون الذي يصف العمليات المتساوية لتوسيع وضغط نظام الغاز. تم إجراء التجارب المقابلة بواسطة روبرت بويل عام 1662 وإدم ماريوت عام 1676. أظهر كل من هؤلاء العلماء بشكل مستقل أنه أثناء عملية متساوية الحرارة في نظام غاز مغلق ، يتغير الضغط عكسيًا مع الحجم. يتم كتابة التعبير الرياضي الذي تم الحصول عليه تجريبياً للعملية بالشكل التالي:
PV=ك
حيث P و V هما الضغط في النظام وحجمه ، k هو نوع من الثبات ، وتعتمد قيمته على كمية مادة الغاز ودرجة حرارتها. إذا قمت ببناء اعتماد دالة P (V) على الرسم البياني ، فسيكون ذلك عبارة عن قطع زائد. ويرد مثال على هذه المنحنيات أدناه.
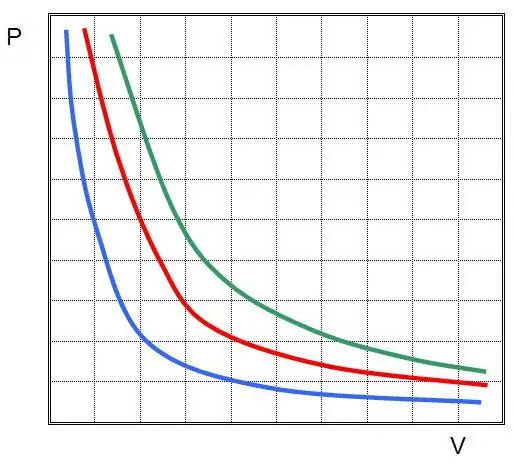
تسمى المساواة المكتوبة بمعادلة بويل ماريوت (قانون). يمكن صياغة هذا القانون بإيجاز على النحو التالي: يؤدي تمدد الغاز المثالي عند درجة حرارة ثابتة إلى انخفاض نسبي في الضغط فيه ، على العكس من ذلك ، يترافق الضغط المتساوي الحرارة لنظام الغاز مع زيادة متناسبة في الضغط فيه.
معادلة الغاز المثالية
قانون Boyle-Mariotte هو حالة خاصة لقانون أكثر عمومية يحمل اسم Mendeleev وكلابيرون. حصل إميل كلابيرون ، الذي يلخص المعلومات التجريبية على سلوك الغازات في ظل ظروف خارجية مختلفة ، في عام 1834 على المعادلة التالية:
PV=nRT
بعبارة أخرى ، ناتج الحجم V لنظام الغاز والضغط P فيه يتناسب طرديًا مع ناتج درجة الحرارة المطلقة T وكمية المادة n. يُشار إلى معامل هذه التناسب بالحرف R ويسمى ثابت الغاز العالمي. في المعادلة المكتوبة ، ظهرت قيمة R نتيجة لاستبدال عدد من الثوابت التي وضعها ديمتري إيفانوفيتش مينديليف في عام 1874.
من المعادلة العامة للحالة ، من السهل أن نرى أن ثبات درجة الحرارة وكمية المادة يضمن ثبات الجانب الأيمن من المعادلة ، مما يعني أن الجانب الأيسر من المعادلة سيبقى أيضًا ثابتًا. في هذه الحالة نحصل على معادلة بويل ماريوت

قوانين الغاز الأخرى
تحتوي معادلة Clapeyron-Mendeleev المكتوبة في الفقرة أعلاه على ثلاث معاملات ديناميكية حرارية: P و V و T. إذا تم إصلاح كل منها ، وسمح للآخرين بالتغيير ، فإننا نحصل على Boyle-Mariotte ، معادلات تشارلز وجاي لوساك. يتحدث قانون تشارلز عن التناسب المباشر بين الحجم ودرجة الحرارة لعملية متساوية الضغط ، وينص قانون جاي لوساك على أنه في حالة الانتقال متساوي الصدور ، فإن ضغط الغاز يزيد أو ينقص بالتناسب المباشر مع درجة الحرارة المطلقة. تبدو المعادلات المقابلة كما يلي:
V / T=const عندما P=const ؛
P / T=const عندما V=const.
هكذاوهكذا ، فإن قانون بويل ماريوت هو أحد قوانين الغاز الثلاثة الرئيسية. ومع ذلك ، فهو يختلف عن الباقي من حيث الاعتماد على الرسوم: الدالتان V (T) و P (T) عبارة عن خطوط مستقيمة ، والوظيفة P (V) عبارة عن قطع زائد.
مثال على مهمة لتطبيق قانون بويل ماريوت
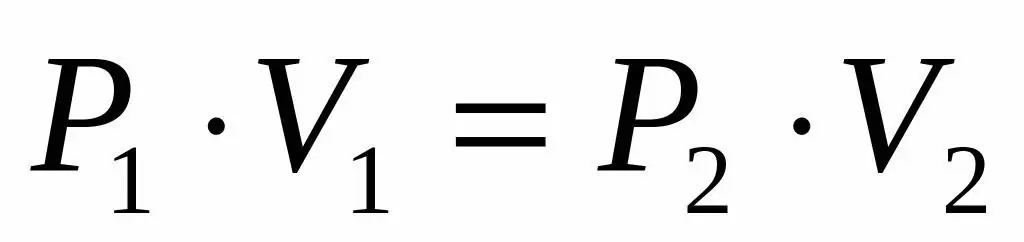
حجم الغاز في الاسطوانة تحت المكبس في الوضع الأولي 2 لتر ، وضغطه 1 جو. كم كان ضغط الغاز بعد ارتفاع المكبس وزاد حجم نظام الغاز بمقدار 0.5 لتر. تعتبر العملية متساوية الحرارة.
بما أننا حصلنا على ضغط وحجم غاز مثالي ، ونعلم أيضًا أن درجة الحرارة تظل دون تغيير أثناء توسعها ، يمكننا استخدام معادلة Boyle-Mariotte بالصيغة التالية:
P1 V1=P2 V2
تقول هذه المساواة أن منتج ضغط الحجم ثابت لكل حالة من الغاز عند درجة حرارة معينة. للتعبير عن القيمة P2من المساواة ، نحصل على الصيغة النهائية:
P2=P1 V1/ V2
عند إجراء حسابات الضغط ، يمكنك استخدام وحدات خارج النظام في هذه الحالة ، لأن اللترات ستتقلص ، ونحصل على الضغط P2في الأجواء. باستبدال البيانات من الحالة ، نصل إلى إجابة سؤال المشكلة: P2=0.8 الغلاف الجوي.






