الظواهر والعمليات الطبيعية من حولنا معقدة للغاية. من أجل الوصف المادي الدقيق ، يجب استخدام جهاز رياضي مرهق ويجب أخذ عدد كبير من العوامل المهمة في الاعتبار. لتجنب هذه المشكلة ، يتم استخدام بعض النماذج المبسطة في الفيزياء ، والتي تسهل بشكل كبير التحليل الرياضي للعملية ، ولكنها لا تؤثر عمليًا على دقة وصفها. واحد منهم هو نموذج الغاز المثالي. دعونا ننظر في الأمر بمزيد من التفصيل في المقال.
مفهوم الغاز المثالي
الغاز المثالي هو حالة تجمع مادة ما ، والتي تتكون من نقاط مادية لا تتفاعل مع بعضها البعض. دعونا نشرح هذا التعريف بمزيد من التفصيل.
أولاً ، نتحدث عن النقاط المادية كأشياء تشكل غازًا مثاليًا. هذا يعني أن جزيئاتها وذراتها ليس لها حجم ، ولكن لها كتلة معينة. إنها جريئةيمكن إجراء تقريب مع الأخذ في الاعتبار حقيقة أنه في جميع الغازات الحقيقية عند ضغوط منخفضة ودرجات حرارة عالية ، تكون المسافة بين الجزيئات أكبر بكثير من أبعادها الخطية.
ثانيًا ، يجب ألا تتفاعل الجزيئات في الغاز المثالي مع بعضها البعض. في الواقع ، توجد مثل هذه التفاعلات دائمًا. لذلك ، حتى ذرات الغازات النبيلة تعاني من جاذبية ثنائية القطب. بمعنى آخر ، تفاعلات van der Waals موجودة. ومع ذلك ، بالمقارنة مع الطاقة الحركية للدوران والحركة الانتقالية للجزيئات ، فإن هذه التفاعلات صغيرة جدًا بحيث لا تؤثر على خصائص الغازات. لذلك ، لا يمكن أخذها في الاعتبار عند حل المشكلات العملية.
من المهم ملاحظة أنه ليس كل الغازات التي تكون فيها الكثافة منخفضة ودرجة الحرارة عالية يمكن اعتبارها مثالية. بالإضافة إلى تفاعلات van der Waals ، هناك أنواع أخرى أقوى من الروابط ، على سبيل المثال ، الروابط الهيدروجينية بين جزيئات H2O ، مما يؤدي إلى انتهاك صارخ لظروف مثالية الغاز. لهذا السبب ، بخار الماء ليس غازاً مثالياً ، لكن الهواء هو.
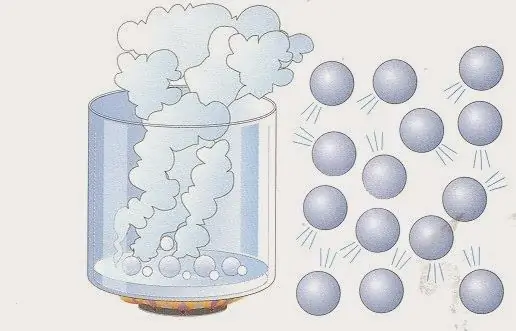
النموذج المادي للغاز المثالي
يمكن تمثيل هذا النموذج على النحو التالي: افترض أن نظام الغاز يحتوي على جزيئات N. يمكن أن تكون هذه ذرات وجزيئات من مواد كيميائية وعناصر مختلفة. عدد الجسيمات N كبير ، لذلك عادة ما تستخدم وحدة "الخلد" لوصفها (1 مول يتوافق مع عدد Avogadro). كلهم يتحركون في بعض الحجم V. حركات الجسيماتفوضوية ومستقلة عن بعضها البعض. لكل منهم سرعة معينة v ويتحرك في مسار مستقيم
نظريًا ، يكون احتمال الاصطدام بين الجسيمات صفرًا تقريبًا ، نظرًا لأن حجمها صغير مقارنة بالمسافات بين الجسيمات. ومع ذلك ، إذا حدث مثل هذا التصادم ، فهو مرن تمامًا. في الحالة الأخيرة ، يتم الحفاظ على الزخم الكلي للجسيمات وطاقتها الحركية.
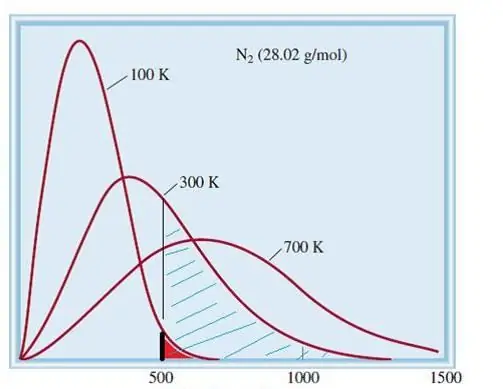
النموذج المدروس للغازات المثالية هو نظام كلاسيكي يحتوي على عدد كبير من العناصر. لذلك ، تخضع سرعة وطاقة الجسيمات الموجودة فيه للتوزيع الإحصائي لماكسويل بولتزمان. بعض الجسيمات لها سرعات منخفضة ، والبعض الآخر سرعات عالية. في هذه الحالة ، يوجد حد معين ضيق للسرعة ، حيث تكمن القيم الأكثر احتمالية لهذه الكمية. يتم عرض توزيع سرعة جزيئات النيتروجين بشكل تخطيطي أدناه.
النظرية الحركية للغازات
نموذج الغازات المثالية الموصوف أعلاه يحدد بشكل فريد خصائص الغازات. تم اقتراح هذا النموذج لأول مرة من قبل دانيال برنولي في عام 1738.

بعد ذلك ، تم تطويره إلى حالته الحالية بواسطة August Kroenig و Rudolf Clausius و Mikhail Lomonosov و James Maxwell و Ludwig Boltzmann و Marian Smoluchowski وعلماء آخرون.
النظرية الحركية للمواد السائلة ، والتي على أساسها تم بناء نموذج الغاز المثالي ، تشرح خاصيتين مجهريتين مهمتين للنظام بناءً على سلوكه المجهري:
- الضغط في الغازات هو نتيجة اصطدام الجسيمات بجدران الوعاء.
- درجة الحرارة في النظام هي نتيجة مظهر من مظاهر الحركة المستمرة للجزيئات والذرات.
دعونا نتوسع في كلا استنتاجي النظرية الحركية.
ضغط الغاز
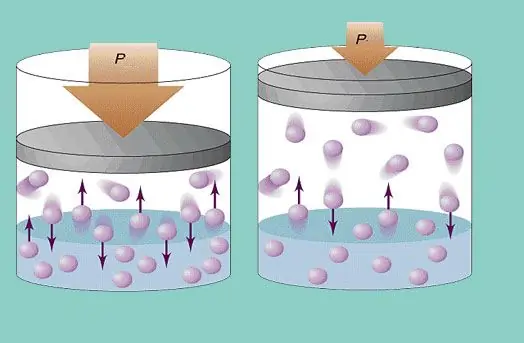
يفترض نموذج الغاز المثالي حركة فوضوية ثابتة للجسيمات في النظام واصطدامها المستمر بجدران الوعاء. كل تصادم من هذا القبيل يعتبر مرنًا تمامًا. كتلة الجسيمات صغيرة (≈10-27-10-25kg). لذلك ، لا يمكن أن يخلق الكثير من الضغط في الاصطدام. ومع ذلك ، فإن عدد الجسيمات ، وبالتالي عدد الاصطدامات ، ضخم (1023). بالإضافة إلى ذلك ، يبلغ جذر متوسط السرعة التربيعية للعناصر عدة مئات من الأمتار في الثانية عند درجة حرارة الغرفة. كل هذا يؤدي إلى إحداث ضغط ملموس على جدران الوعاء. يمكن حسابه باستخدام الصيغة التالية:
P=Nmvcp2/ (3V) ،
حيث vcpهو جذر متوسط السرعة التربيعية ، m هو كتلة الجسيمات.
درجة الحرارة المطلقة
وفقًا لنموذج الغاز المثالي ، يتم تحديد درجة الحرارة بشكل فريد من خلال متوسط الطاقة الحركية لجزيء أو ذرة في النظام قيد الدراسة. يمكنك كتابة التعبير التالي الذي يربط بين الطاقة الحركية ودرجة الحرارة المطلقة للغاز المثالي:
mvcp2/ 2=3/2kB T.
هنا kBهو ثابت بولتزمان. من هذه المساواة نحصل على:
T=م vcp2/ (3kB).
معادلة الحالة العالمية
إذا قمنا بدمج التعبيرات أعلاه للضغط المطلق P ودرجة الحرارة المطلقة T ، فيمكننا كتابة المساواة التالية:
PV=nRT.
هنا n هي كمية المادة في المولات ، R هو ثابت الغاز الذي قدمه D. I. Mendeleev. هذا التعبير هو أهم معادلة في نظرية الغازات المثالية ، لأنه يجمع بين ثلاث معاملات ديناميكية حرارية (V ، P ، T) ولا يعتمد على الخصائص الكيميائية لنظام الغاز.

تم اشتقاق المعادلة العالمية تجريبياً لأول مرة من قبل الفيزيائي الفرنسي إميل كلابيرون في القرن التاسع عشر ثم تم إدخالها إلى شكلها الحديث بواسطة الكيميائي الروسي منديليف ، ولهذا السبب تحمل حاليًا أسماء هؤلاء العلماء.






