الغاز المثالي ، معادلة الغاز المثالية للحالة ودرجة حرارته وضغطه وحجمه … يمكن متابعة قائمة المعلمات والتعريفات المستخدمة في القسم المقابل من الفيزياء لفترة طويلة جدًا. اليوم سنتحدث فقط عن هذا الموضوع
ما الذي يعتبر في الفيزياء الجزيئية؟

العنصر الرئيسي الذي تم تناوله في هذا القسم هو الغاز المثالي. تم الحصول على معادلة الغاز المثالية للحالة مع مراعاة الظروف البيئية العادية ، وسنتحدث عن هذا بعد قليل. الآن دعونا نتعامل مع هذه "المشكلة" من بعيد.
لنفترض أن لدينا بعض كتلة الغاز. يمكن تحديد حالتها باستخدام ثلاث معلمات ذات طبيعة ديناميكية حرارية. هذه بالطبع هي الضغط والحجم ودرجة الحرارة. ستكون معادلة حالة النظام في هذه الحالة هي صيغة العلاقة بين المعلمات المقابلة. يبدو كالتالي: F (p، V، T)=0.
هنا ، ولأول مرة ، نقترب ببطء من ظهور شيء مثل المثاليغاز. يطلق عليه غازا تكون فيه التفاعلات بين الجزيئات ضئيلة. بشكل عام ، هذا غير موجود في الطبيعة. ومع ذلك ، فإن أي غاز شديد التخلخل يكون قريبًا منه. يختلف النيتروجين والأكسجين والهواء ، في الظروف العادية ، قليلاً عن المثالي. لكتابة معادلة الحالة للغاز المثالي ، يمكننا استخدام قانون الغاز الموحد. نحصل على: pV / T=const.
المفهوم ذو الصلة رقم 1: قانون أفوجادرو
يمكنه أن يخبرنا أنه إذا أخذنا نفس عدد مولات أي غاز عشوائي تمامًا ووضعناها في نفس الظروف ، بما في ذلك درجة الحرارة والضغط ، فإن الغازات ستشغل نفس الحجم. على وجه الخصوص ، أجريت التجربة في ظل ظروف طبيعية. هذا يعني أن درجة الحرارة كانت 273.15 كلفن ، والضغط كان جوًا واحدًا (760 ملم زئبق ، أو 101325 باسكال). باستخدام هذه المعلمات ، احتل الغاز حجمًا يساوي 22.4 لترًا. لذلك ، يمكننا القول أنه بالنسبة لمول واحد من أي غاز ، ستكون نسبة المعلمات العددية قيمة ثابتة. لهذا السبب تقرر تعيين هذا الرقم بالحرف R وتسميته بثابت الغاز العام. وبالتالي ، فهي تساوي 8.31. الوحدة هي J / molK.
غاز مثالي. معادلة الغاز المثالية للحالة والتلاعب بها
دعونا نحاول إعادة كتابة الصيغة. للقيام بذلك ، نكتبه على هذا النحو: pV=RT. بعد ذلك ، نقوم بإجراء بسيط ، نضرب طرفي المعادلة بعدد عشوائي من الشامات. نحصل على pVu=uRT. دعونا نأخذ في الاعتبار حقيقة أن حاصل ضرب الحجم المولي ومقدار المادة هو ببساطة الحجم. ولكن في النهاية ، سيكون عدد المولات مساويًا لحاصل قسمة الكتلة والكتلة المولية في نفس الوقت. هذا هو بالضبط ما تبدو عليه معادلة مندليف - كلابيرون. إنه يعطي فكرة واضحة عن نوع النظام الذي يشكله الغاز المثالي. ستأخذ معادلة الحالة للغاز المثالي الشكل: pV=mRT / M.
استنتج صيغة الضغط
لنقم ببعض التلاعبات مع التعبيرات التي تم الحصول عليها. للقيام بذلك ، يتم ضرب الجانب الأيمن من معادلة Mendeleev-Clapeyron وقسمته على رقم Avogadro. الآن ننظر بعناية إلى منتج كمية المادة برقم Avogadro. هذا ليس سوى العدد الإجمالي للجزيئات في الغاز. لكن في الوقت نفسه ، ستكون نسبة ثابت الغاز العالمي إلى رقم أفوجادرو مساوية لثابت بولتزمان. لذلك ، يمكن كتابة معادلات الضغط على النحو التالي: p=NkT / V أو p=nkT. هنا الرمز n هو تركيز الجسيمات.
عمليات الغاز المثالية
في الفيزياء الجزيئية يوجد شيء مثل المعالجات المتشابهة. هذه هي العمليات الديناميكية الحرارية التي تحدث في النظام بأحد المعلمات الثابتة. في هذه الحالة ، يجب أن تظل كتلة المادة ثابتة أيضًا. دعونا ننظر إليهم بشكل أكثر تحديدًا. اذن قوانين الغازات المثالية
الضغط يبقى ثابتًا
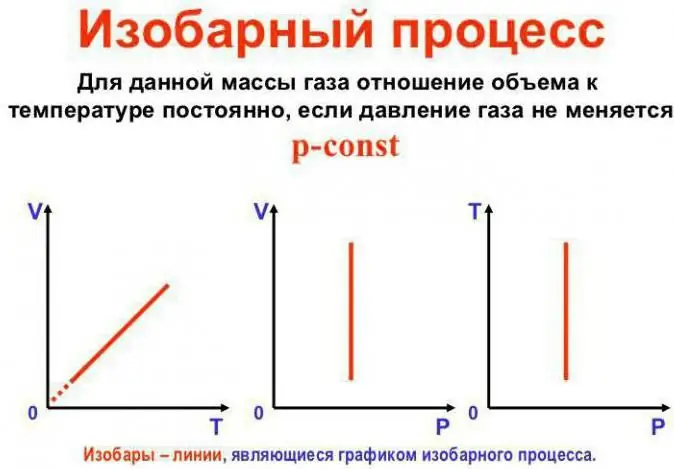
هذا هو قانون جاي لوساك. يبدو مثل هذا: V / T=const. يمكن إعادة كتابته بطريقة أخرى: V=Vo (1 + at). هنا a يساوي 1 / 273.15 K ^ -1 ويسمى "معامل تمدد الحجم". يمكننا التعويض عن درجة الحرارة بالقيمتين المئويتين ومقياس كلفن. في الحالة الأخيرة ، نحصل على الصيغة V=Voat.
الحجم يبقى ثابتًا

هذا هو قانون جاي لوساك الثاني ، ويشار إليه أكثر بقانون تشارلز. يبدو مثل هذا: p / T=const. هناك صيغة أخرى: p=po (1 + at). يمكن إجراء التحويلات وفقًا للمثال السابق. كما ترى ، فإن قوانين الغاز المثالية تكون أحيانًا متشابهة تمامًا مع بعضها البعض.
درجة الحرارة تبقى ثابتة

إذا ظلت درجة حرارة الغاز المثالي ثابتة ، فيمكننا الحصول على قانون بويل ماريوت. يمكن كتابتها على النحو التالي: pV=const.
المفهوم ذو الصلة رقم 2: الضغط الجزئي
لنفترض أن لدينا وعاء به غازات. سيكون خليط. النظام في حالة توازن حراري ، والغازات نفسها لا تتفاعل مع بعضها البعض. هنا سيشير N إلى العدد الإجمالي للجزيئات. N1 و N2 وما إلى ذلك ، على التوالي ، عدد الجزيئات في كل مكون من مكونات الخليط. لنأخذ صيغة الضغط p=nkT=NkT / V. يمكن فتحه لحالة معينة. بالنسبة للخليط المكون من مكونين ، ستتخذ الصيغة الشكل: p=(N1 + N2) kT / V. ولكن بعد ذلك اتضح أن الضغط الكلي سيتم تلخيصه من الضغوط الجزئية لكل خليط. لذلك ، سيبدو مثل p1 + p2 وما إلى ذلك. ستكون هذه ضغوط جزئية.
ما هذا؟
تشير الصيغة التي حصلنا عليها إلى أن الضغط في النظام يأتي من كل مجموعة من الجزيئات. بالمناسبة ، فإنه لا يعتمد علىالآخرين. استفاد دالتون من هذا عند صياغة القانون ، الذي سُمي لاحقًا باسمه: في خليط حيث لا تتفاعل الغازات كيميائيًا مع بعضها البعض ، سيكون الضغط الكلي مساويًا لمجموع الضغوط الجزئية.






