الديناميكا الحرارية للحالة التجميعية الغازية للمادة هي فرع مهم من فروع الفيزياء التي تدرس التوازن الديناميكي الحراري والانتقالات شبه الساكنة في الأنظمة. النموذج الرئيسي الذي تستند إليه تنبؤات سلوك الأنظمة هو نموذج الغاز المثالي. مع استخدامه ، تم الحصول على معادلة مندليف - كلابيرون. اعتبرها في المقال
الغاز المثالي
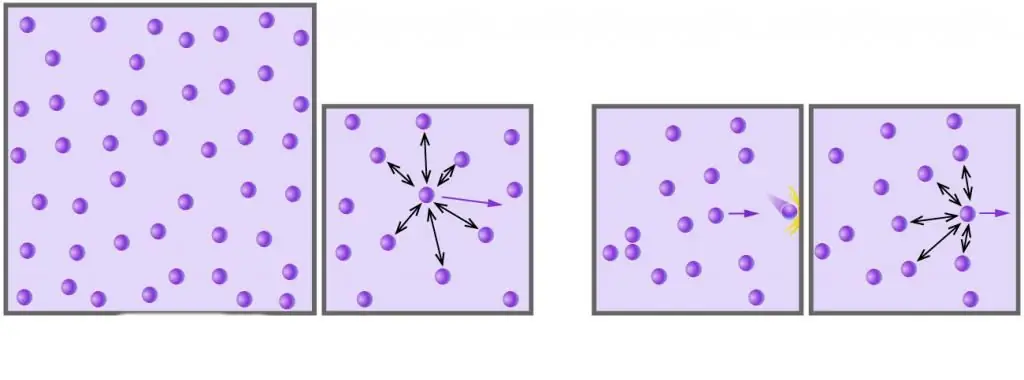
كما تعلم ، تتكون جميع الغازات الحقيقية من جزيئات أو ذرات ، والمسافات بينها كبيرة جدًا مقارنة بحجمها عند الضغط المنخفض. بالإضافة إلى ذلك ، في درجات الحرارة المرتفعة ، على نطاق مطلق ، تتجاوز الطاقة الحركية للجزيئات طاقتها الكامنة المرتبطة بتفاعلات ثنائية القطب ضعيفة (إذا كان هناك ، بالإضافة إلى هذه التفاعلات ، أنواع أخرى من الروابط الكيميائية ، على سبيل المثال ، أيوني أو الهيدروجين ، ثم يساهمون بشكل كبير في المكون المحتمل لطاقة النظام الداخلي).
بسبببالنسبة للعديد من الغازات الحقيقية في ظل ظروف قريبة من المعتاد ، يمكن للمرء إهمال تفاعلاتها الداخلية وأحجام الجسيمات. يشكل هذان التقريبان الرئيسيان نموذج الغاز المثالي.
معادلة مندليف في الفيزياء

من الأصح والإنصاف تسمية هذه المعادلة بقانون Clapeyron-Mendeleev. الحقيقة هي أنه تم تسجيله لأول مرة من قبل المهندس الفرنسي إميل كلابيرون في عام 1834. لقد فعل ذلك من خلال تحليل قوانين الغاز الخاصة بويل ماريوت وجاي-لوساك وتشارلز التي اكتشفها في بداية القرن التاسع عشر.
تكمن ميزة الكيميائي الروسي دميتري مينديليف في حقيقة أنه أعطى المعادلة شكلًا رياضيًا حديثًا وسهل الاستخدام. على وجه الخصوص ، أدخل Mendeleev في المعادلة ثابتًا لجميع الغازات R=8 ، 314 J / (molK). استخدم كلابيرون نفسه عددًا من الثوابت التجريبية التي تجعل العملية الحسابية صعبة.
تتم كتابة معادلة مندليف-كلابيرون على النحو التالي:
PV=nRT.
تعني هذه المساواة أن ناتج الضغط P والحجم V على الجانب الأيسر من التعبير يتناسب دائمًا مع ناتج درجة الحرارة المطلقة T وكمية المادة n على الجانب الأيسر.
يسمح لك التعبير قيد الدراسة بالحصول على أي قانون غاز إذا قمت بإصلاح اثنين من معلماته الأربعة. في حالة المعالجات المتساوية ، تتم دراسة الأنظمة المغلقة التي لا يوجد فيها تبادل للمادة مع البيئة (n=const). تتميز هذه العمليات بمعامل حراري ديناميكي ثابت واحد (T ، P أو V).

مثال على المشكلة
الآن دعونا نحل المشكلة في معادلة مندليف - كلابيرون. من المعروف أن الأكسجين الذي يزن 500 جرام يوجد في أسطوانة بحجم 100 لتر عند ضغط 2 جو. ما هي درجة الحرارة في البالون ، مع العلم أن النظام في حالة توازن ديناميكي حراري.
تذكر أنه وفقًا للتعريف ، يتم حساب كمية المادة بواسطة الصيغة:
n=م / م
حيث m هي كتلة جميع جسيمات النظام ، M هي متوسط كتلتها المولية. تسمح لنا هذه المساواة بإعادة كتابة معادلة منديليف بالشكل التالي:
PV=مRT / M.
من أين نحصل على صيغة العمل لهذه المهمة:
T=PVM / (مص).
يبقى تحويل جميع الكميات إلى وحدات SI واستبدالها في هذا التعبير:
T=21013250، 10، 032 / (0، 58، 314)=156 ك
درجة الحرارة المحسوبة هي -117oC. على الرغم من أن الأكسجين عند درجة الحرارة هذه لا يزال غازيًا (يتكثف عند -182.96oC) ، في ظل هذه الظروف ، لا يمكن استخدام نموذج الغاز المثالي إلا للحصول على تقدير نوعي للقيمة المحسوبة.






