ثنائي القطب الكهربائي. فيزياء الصف العاشر. الديناميكا الكهربائية

2024 مؤلف: Angel Austin | [email protected]. آخر تعديل: 2024-01-02 17:40

عند دراسة الفيزياء في الصف العاشر ، يتم النظر في موضوع ثنائيات الأقطاب. ماذا يعني هذا المفهوم وما الصيغ المستخدمة لحسابه؟

مقدمة

إذا وضعت ثنائي القطب في مساحة مجال كهربائي موحد ، فيمكنك تمثيله كخطوط قوة. ثنائي القطب هو نظام توجد فيه شحنتان متطابقتان في المعلمات ، لكنهما شحنة نقطية معاكسة. علاوة على ذلك ، فإن المسافة بينهما ستكون أقل بكثير من المسافة إلى أي نقطة في المجال ثنائي القطب. تمت دراسة مفهوم العزم ثنائي القطب في الدورة المدرسية للديناميكا الكهربائية (الصف 10).

محور ثنائي القطب هو خط مستقيم يمر عبر نقطتي الشحنتين. الذراع ثنائي القطب عبارة عن ناقل يربط شحنة وفي نفس الوقت ينتقل من جسيمات سالبة الشحنة إلى جسيمات موجبة الشحنة. يتميز ثنائي القطب الكهربائي بوجود حالة مثل ثنائي القطب أو عزم كهربائي.

حسب التعريف ، العزم ثنائي القطب هو متجه يساوي عدديًا منتج الشحنة ثنائية القطب وذراعها. علاوة على ذلك ، يتم توجيهه بشكل مشترك مع كتف ثنائي القطب. عند المساواة الصفرية لمجموع القوى ، نحسب قيمة اللحظة. للزاوية الموجودة بين العزم ثنائي القطب واتجاهية المجال الكهربائي ، وجود لحظة ميكانيكية مميزة

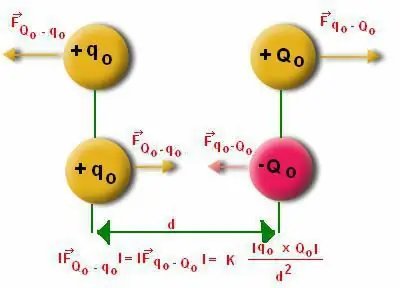
غالبًا ما يجد الناس صعوبة في حساب المعامل الذي يعمل على هيكل ثنائي القطب. من الضروري هنا مراعاة خصوصيات حساب الزاوية "ألفا". من المعروف أن ثنائي القطب ينحرف عن الوضع المتوازن. لكن العزم ثنائي القطب نفسه له طابع استعادة ، لأنه يميل إلى الحركة.

الحسابات

عندما يتم وضع هذه العزم ثنائي القطب في وسط مجال كهربائي غير متجانس ، تنشأ قوة لا محالة. في مثل هذه البيئة ، لن تكون مؤشرات مجموع القوى صفرًا. وبالتالي ، هناك قوى تعمل على العزم ثنائي القطب ذات طابع نقطي. حجم الذراع ثنائي القطب أصغر بكثير.

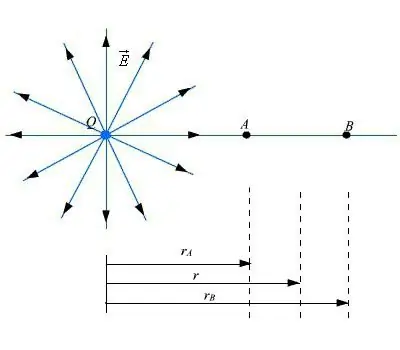
يمكن كتابة الصيغة على النحو التالي: F=q (E2 - E1)=qdE ، حيث d هو فرق المجال الكهربائي.

ابحث عن خصائص المفهوم المادي قيد الدراسة

دعونا نلقي نظرة أكثر على الموضوع. من أجل تحديد ما هي خاصية المجال الكهربائي ، إذا تم إنشاؤه باستخدام نظام الشحن والموقع في مساحة صغيرة ، فمن الضروري إجراء عدد من الحسابات. يتم تقديم مثال عن طريق الذرات والجزيئات ، والتي تحتوي في تركيبها على نوى وإلكترونات مشحونة كهربائيًا.

إذا كان من الضروري البحث عن حقل على مسافة أكبر من الأبعاد التي تشكل المنطقة التي توجد بها الجسيمات ، فسنستخدم عددًا من الصيغ الدقيقة المعقدة للغاية. من الممكن استخدام أبسطتعابير تقريبية. لنفترض أن مجموعات النقاط من الشحنات q_{kتشارك في إنشاء المجال الكهربائي. تقع في مساحة صغيرة}

لإجراء حساب الخاصية التي يمتلكها الحقل ، يُسمح بدمج جميع رسوم النظام. يعتبر مثل هذا النظام بمثابة شحنة نقطية Q. ستكون مؤشرات الحجم هي مجموع الرسوم التي كانت في النظام الأصلي.

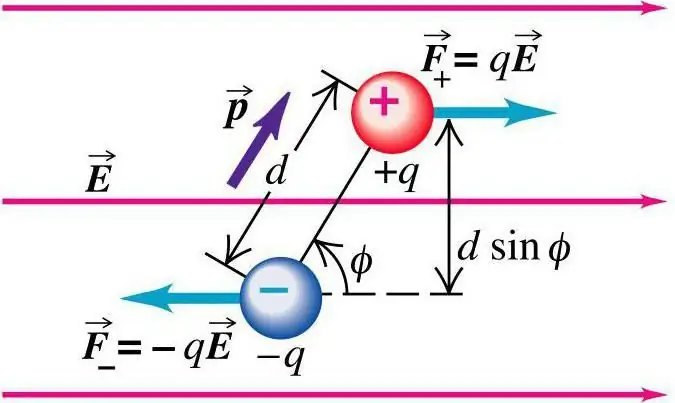
موقع الرسوم

دعونا نتخيل أن موقع الشحنة محدد في أي مكان يوجد فيه نظام الرسوم q_{k. عند إجراء تغييرات على الموقع ، إذا كان له حدود معبر عنها في منطقة صغيرة ، فسيكون هذا التأثير ضئيلًا ، وغير محسوس تقريبًا للمجال من وجهة النظر. ضمن هذه الحدود التقريبية للقوة والإمكانات التي يمتلكها المجال الكهربائي ، يتم إجراء التحديدات باستخدام الصيغ التقليدية.}

عندما يكون مجموع الشحنة الإجمالية للنظام صفرًا ، ستبدو معلمات التقريب المشار إليه تقريبية. هذا يعطي سببًا لاستنتاج أن المجال الكهربائي ببساطة غائب. إذا كان من الضروري الحصول على تقريب أكثر دقة ، اجمع عقليًا مجموعات منفصلة من الشحنات الموجبة والسالبة للنظام الذي يتم النظر فيه.

في حالة إزاحة "مراكزهم" بالنسبة إلى الآخرين ، يمكن وصف معلمات المجال في مثل هذا النظام على أنها حقل به شحنتان نقطيتان متساويتان في الحجم ومعاكسة للإشارة. ويلاحظ أنهم مشردون فيما يتعلق بالآخرين. ليزودللحصول على توصيف أكثر دقة لنظام الشحنات من حيث معاملات هذا التقريب ، سيكون من الضروري دراسة خصائص ثنائي القطب في مجال كهربائي.

مقدمة للمصطلح

دعنا نعود إلى التعريف. ثنائي القطب الكهربائي هو تعريف النظام الذي يشتمل على شحنتين نقطيتين. لديهم نفس الحجم والعلامات المعاكسة. علاوة على ذلك ، تقع هذه العلامات على مسافات صغيرة مقارنة بعلامات أخرى.

يمكنك حساب خاصية العملية التي يتم إنشاؤها عن طريق ثنائي القطب ، ويتم تمثيلها بشحنتين نقطتين: + q و q ، وتقعان على مسافة قريبة من الآخرين.

تسلسل العمليات الحسابية

لنبدأ بحساب الجهد والشدة التي يمتلكها ثنائي القطب على سطحه المحوري. هذا خط مستقيم بين شحنتين. بشرط أن تقع النقطة A على مسافة تساوي r بالنسبة للجزء المركزي من ثنائي القطب ، وإذا كانت r >> a ، وفقًا لمبدأ التراكب لإمكانات المجال عند هذه النقطة ، فسيكون ذلك منطقيًا استخدم التعبير لحساب معلمات ثنائي القطب.

يتم حساب حجم متجه القوة من خلال مبدأ التراكب.لحساب شدة المجال ، يتم استخدام مفهوم نسبة الجهد وشدة المجال:

E_{x=−Δφ /Δx.}

في ظل هذه الظروف ، يشار إلى اتجاه متجه الكثافة طوليًا بالنسبة لمحور ثنائي القطب. لحساب معاملها ، فإن الصيغة القياسية قابلة للتطبيق.

هامتوضيحات

يجب أن يؤخذ في الاعتبار أن ضعف المجال الكهربائي ثنائي القطب يحدث بشكل أسرع من تعرضه لشحنة نقطية. يتناسب اضمحلال جهد المجال ثنائي القطب عكسياً مع مربع المسافة ، وتتناسب شدة المجال عكسياً مع مكعب المسافة.

باستخدام طرق مماثلة ، ولكن أكثر تعقيدًا ، تم العثور على معلمات الجهد وشدة المجال ثنائي القطب في نقاط عشوائية ، يتم تحديد معلمات الموضع باستخدام طريقة الحساب مثل الإحداثيات القطبية: المسافة إلى مركز ثنائي القطب (ص) والزاوية ()

الحساب باستخدام متجه التوتر

ينقسم مفهوم متجه الكثافة E إلى نقطتين:

• شعاعي (E_{r) ، وهو موجه في الاتجاه الطولي بالنسبة للخط المستقيم.}
• مثل هذا الخط المستقيم يربط النقطة المحددة ومركز ثنائي القطب مع عمودي عليه E_θ.

يتم توجيه هذا التحلل لكل مكون على طول مسار التغيير الذي يحدث مع جميع إحداثيات النقطة المراد ملاحظتها. يمكنك العثور عليه من خلال النسبة التي تربط مؤشرات قوة المجال بالتعديلات المحتملة.

العثور على مكون المتجه عند شدة المجال ، من المهم تحديد طبيعة العلاقة في التغييرات المحتملة التي تحدث بسبب إزاحة نقطة المراقبة في اتجاه المتجهات.

احسب المكون العمودي

عند الانتهاءبالنسبة لهذا الإجراء ، من المهم أن نأخذ في الاعتبار أن التعبير عن المقدار عند إزاحة صغيرة عمودية سيتم تحديدها عن طريق تغيير الزاوية: Δl=rΔθ.ستكون معلمات الحجم لمكون المجال هذا متساوية.

بعد الحصول على النسبة ، من الممكن تحديد مجال ثنائي القطب الكهربائي عند نقطة عشوائية لبناء صورة بخطوط القوة لهذا المجال.

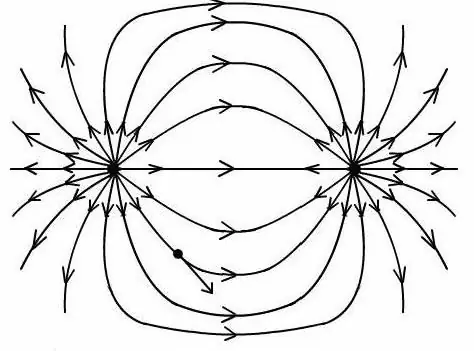
من المهم مراعاة أن جميع الصيغ لتحديد الإمكانات وشدة المجال لثنائي القطب تعمل فقط على ناتج قيم الشحنة ثنائية القطب الواحدة والمسافة بينها.

لحظة ثنائية القطب

عنوان العمل الموصوف هو وصف كامل لنوع الخصائص الكهربائية. لها اسم "العزم ثنائي القطب للنظام".

من خلال تعريف ثنائي القطب ، وهو نظام من الشحنات النقطية ، يمكن معرفة أنه يتميز بوجود تناظر محوري ، عندما يكون المحور خطًا مستقيمًا يمر بعدة شحنات.

لتعيين الخصائص الكاملة لثنائي القطب ، حدد اتجاه الاتجاه الذي يحتوي عليه المحور. لتبسيط العمليات الحسابية ، يمكن تحديد متجه العزم ثنائي القطب. قيمة حجمه تساوي حجم العزم ثنائي القطب ، ويختلف متجه الاتجاه عن طريق تزامنه مع محور ثنائي القطب. لذلك ، p=qa إذا كان a هو اتجاه المتجه الذي يربط الشحنات السالبة والموجبة للثنائي القطب.

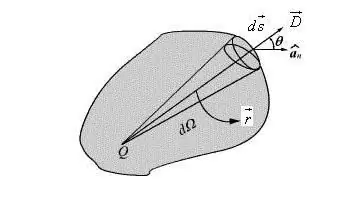
استخدام مثل هذه الخاصية من ثنائي القطب ملائم ويجعل من الممكن في معظم الحالات تبسيط الصيغة وإعطائها الشكلالمتجه. وصف إمكانات المجال ثنائي القطب عند نقطة اتجاه تعسفي مكتوب في شكل متجه.

يمكن تنفيذ إدخال مفاهيم مثل الخاصية المتجهية لثنائي القطب وعزمه ثنائي القطب باستخدام نموذج مبسط - شحنة نقطية في مجال موحد ، والذي يتضمن نظامًا للشحنات ، والأبعاد الهندسية لها علاقة لا يجب أن تؤخذ في الاعتبار ، ولكن من المهم معرفة العزم ثنائي القطب. هذا شرط أساسي لإجراء العمليات الحسابية.

كيف يتصرف ثنائي القطب

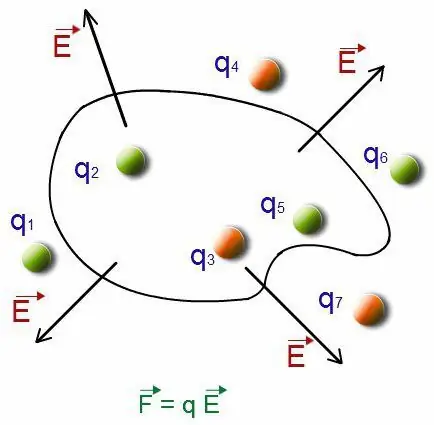
يمكن رؤية سلوك ثنائي القطب في مثال مثل هذه الحالة. موضع شحنتين نقطتين له طابع ثابت للمسافة بالنسبة لبعضهما البعض. تم وضعهم في ظروف ثنائي القطب في مجال كهربائي موحد. أدلى ملاحظات على العملية. في دروس الفيزياء (الديناميكا الكهربائية) ، يتم النظر في هذا المفهوم بالتفصيل. من الميدان إلى الشحنة ، يتم تنفيذ عمل القوات:

F=± qE

هم متساوون في الحجم وعكس الاتجاه. مؤشر القوة الكلية التي تعمل على ثنائي القطب هو صفر. نظرًا لأن مثل هذه القوة لها تأثير على نقاط مختلفة ، فإن اللحظة الإجمالية ستكون:

M=Fa sin a=qEa sin a=pE sin a

حيث تكون α هي الزاوية التي تربط متجهات شدة المجال ومتجهات العزم ثنائي القطب. نظرًا لوجود لحظة القوة ، فإن العزم ثنائي القطب للنظام يميل إلى العودة إلى اتجاهات متجه شدة المجال الكهربائي.

ثنائي القطب الكهربائي مفهوم مهم لفهمه بوضوح. يمكنك قراءة المزيد عنها على الإنترنت. كما يمكنللدراسة في دروس الفيزياء بالمدرسة في الصف العاشر كما تحدثنا أعلاه.