دراسة العمليات التي تحدث في النظم الإحصائية معقدة بسبب الحجم الأدنى للجسيمات وعددها الضخم. من المستحيل عمليا النظر في كل جسيم على حدة ، لذلك يتم إدخال كميات إحصائية: متوسط سرعة الجسيمات ، وتركيزها ، وكتلة الجسيمات. تسمى الصيغة التي تميز حالة النظام ، مع الأخذ في الاعتبار المعلمات المجهرية ، المعادلة الأساسية للنظرية الحركية الجزيئية للغازات (MKT).
قليلا عن متوسط سرعة الجسيمات
تم تحديد سرعة الجسيمات لأول مرة بشكل تجريبي. أتاحت تجربة معروفة من المناهج الدراسية ، أجراها أوتو ستيرن ، تكوين فكرة عن سرعات الجسيمات. أثناء التجربة ، تمت دراسة حركة ذرات الفضة في الأسطوانات الدوارة: أولاً ، في حالة ثابتة من التثبيت ، ثم عندما تدور بسرعة زاوية معينة.
نتيجة لذلك وجد أن سرعة جزيئات الفضة تتجاوز سرعة الصوت وهي 500 م / ث. الحقيقة مثيرة للاهتمام ، لأنه من الصعب على الشخص أن يشعر بمثل هذه السرعات في حركة الجسيمات في المواد.
الغاز المثالي
مواصلة البحثيبدو ممكنًا فقط في نظام يمكن تحديد معلماته من خلال القياسات المباشرة باستخدام الأدوات المادية. تُقاس السرعة بمقياس سرعة ، لكن فكرة ربط عداد السرعة بجسيم واحد هي فكرة سخيفة. فقط المعلمة العيانية المرتبطة بحركة الجسيمات يمكن قياسها مباشرة.
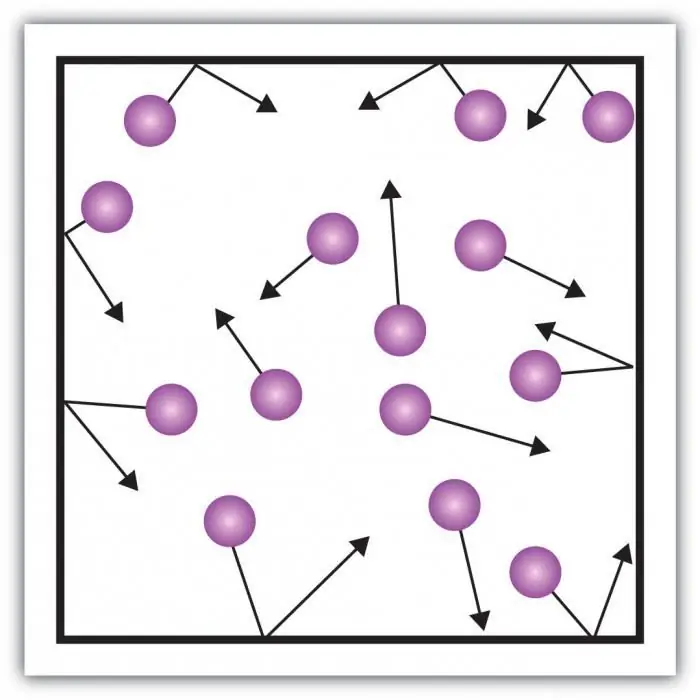
ضع في اعتبارك ضغط الغاز. ينتج الضغط على جدران الوعاء عن تأثيرات جزيئات الغاز في الوعاء. تكمن خصوصية الحالة الغازية للمادة في مسافات كبيرة بدرجة كافية بين الجسيمات وتفاعلها الصغير مع بعضها البعض. هذا يسمح لك بقياس ضغطه مباشرة.
أي نظام من الأجسام المتفاعلة يتميز بالطاقة الكامنة والطاقة الحركية للحركة. الغاز الحقيقي هو نظام معقد. تقلب الطاقة الكامنة لا يصلح للتنظيم. يمكن حل المشكلة من خلال تقديم نموذج يحمل الخصائص المميزة للغاز ، مع التخلص من تعقيد التفاعل.
الغاز المثالي هو حالة مادة يكون فيها تفاعل الجسيمات ضئيلًا ، وتميل الطاقة الكامنة للتفاعل إلى الصفر. فقط طاقة الحركة ، التي تعتمد على سرعة الجسيمات ، يمكن اعتبارها ذات أهمية.
ضغط الغاز المثالي
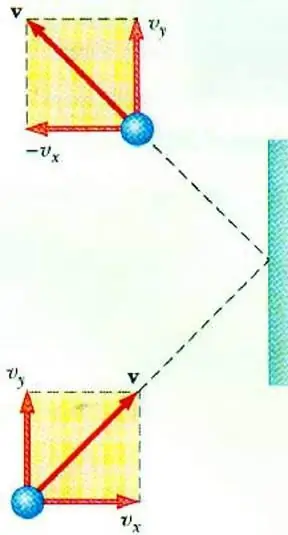
للكشف عن العلاقة بين ضغط الغاز وسرعة جزيئاته يسمح بالمعادلة الأساسية لـ MKT للغاز المثالي. الجسيم المتحرك في وعاء ، عند الاصطدام بالجدار ، ينقل إليه دفعة ، يمكن تحديد قيمتها على أساس القانون الثانينيوتن:
F∆t=2m0vx
يرتبط التغيير في زخم الجسيم أثناء التأثير المرن بتغير في المكون الأفقي لسرعته. F هي القوة المؤثرة من جانب الجسيم على الحائط لفترة قصيرة t ؛ م0 - كتلة الجسيمات.
تتصادم جميع جزيئات الغاز مع سطح المنطقة S خلال الوقت ∆t ، وتتحرك في اتجاه السطح بسرعة vxوتقع في أسطوانة بحجم Sυx Δt. عند تركيز الجسيمات n ، يتحرك نصف الجزيئات بالضبط نحو الجدار ، بينما يتحرك النصف الآخر في الاتجاه المعاكس.
بعد النظر في تصادم جميع الجسيمات ، يمكننا كتابة قانون نيوتن للقوة المؤثرة على المنطقة:
F∆t=nm0vx2S∆t
نظرًا لتعريف ضغط الغاز على أنه نسبة القوة المؤثرة عموديًا على السطح إلى مساحة الأخير ، يمكننا كتابة:
p=F: S=nm0vx2
العلاقة الناتجة مثل المعادلة الأساسية لـ MKT لا يمكن أن تصف النظام بأكمله ، حيث يتم النظر في اتجاه واحد فقط للحركة.
توزيع ماكسويل
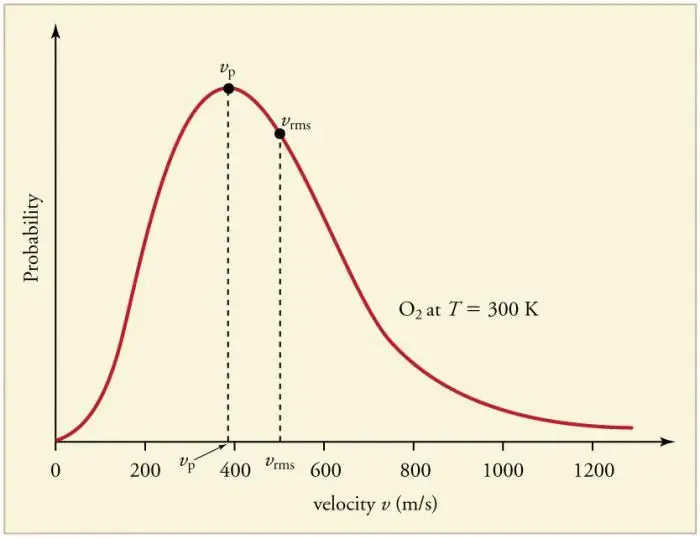
الاصطدامات المتكررة المستمرة لجزيئات الغاز مع الجدران ومع بعضها البعض تؤدي إلى إنشاء توزيع إحصائي معين للجسيمات من حيث السرعات (الطاقات). اتضح أن اتجاهات جميع متجهات السرعة متساوية في الاحتمال. يسمى هذا التوزيع توزيع ماكسويل. في عام 1860 كان هذا النمطمستمدة من ج. ماكسويل على أساس MKT. تسمى المعلمات الرئيسية لقانون التوزيع بالسرعات: محتمل ، يتوافق مع القيمة القصوى للمنحنى ، وجذر متوسط المربع vkv=√ ‹v 2›- متوسط مربع سرعة الجسيم.
ارتفاع درجة حرارة الغاز يتوافق مع زيادة السرعة.
بناءً على حقيقة أن جميع السرعات متساوية وأن وحداتها لها نفس القيمة ، يمكننا أن نفترض:
‹v2 ›=‹vx2 › + ‹v y2›+‹ vz2›، من:‹ vx2›=‹ v2›: 3
المعادلة الأساسية لـ MKT ، مع مراعاة متوسط قيمة ضغط الغاز ، هي:
p=nm0‹v2 ›: 3.
هذه العلاقة فريدة من نوعها من حيث أنها تحدد العلاقة بين المعلمات المجهرية: السرعة وكتلة الجسيمات وتركيز الجسيمات وضغط الغاز بشكل عام.
باستخدام مفهوم الطاقة الحركية للجسيمات ، يمكن إعادة كتابة المعادلة الأساسية لـ MKT بشكل مختلف:
p=2nm0‹v2 ›: 6=2n ‹Ek ›: 3
يتناسب ضغط الغاز مع متوسط قيمة الطاقة الحركية لجزيئاته.
درجة الحرارة
ومن المثير للاهتمام ، أنه للحصول على كمية ثابتة من الغاز في وعاء مغلق ، يمكن للمرء أن يربط بين ضغط الغاز ومتوسط قيمة طاقة حركة الجسيمات. في هذه الحالة ، يمكن قياس الضغط عن طريق قياس الطاقةالجسيمات.
ماذا تفعل؟ ما هي القيمة التي يمكن مقارنتها بالطاقة الحركية؟ تبين أن درجة الحرارة مثل هذه القيمة.

درجة الحرارة هي مقياس للحالة الحرارية للمواد. لقياسه ، يتم استخدام مقياس حرارة ، أساسه هو التمدد الحراري لسائل العمل (كحول ، زئبق) عند تسخينه. يتم إنشاء مقياس الحرارة بشكل تجريبي. عادة ، يتم وضع علامات عليه مطابقة لموضع سائل العمل أثناء بعض العمليات الفيزيائية التي تحدث في حالة حرارية ثابتة (الماء المغلي ، ذوبان الجليد). موازين الحرارة المختلفة لها مقاييس مختلفة. على سبيل المثال ، مئوية ، فهرنهايت.

مقياس درجة الحرارة العالمي
يمكن اعتبار موازين الحرارة الغازية أكثر إثارة للاهتمام من حيث الاستقلال عن خصائص مائع العمل. لا يعتمد حجمها على نوع الغاز المستخدم. في مثل هذا الجهاز ، يمكن للمرء افتراضيًا تحديد درجة الحرارة التي يميل فيها ضغط الغاز إلى الصفر. تظهر الحسابات أن هذه القيمة تتوافق مع -273.15oC. تم تقديم مقياس درجة الحرارة (مقياس درجة الحرارة المطلقة أو مقياس كلفن) في عام 1848. تم أخذ درجة الحرارة المحتملة لضغط الغاز الصفري كنقطة رئيسية في هذا المقياس. جزء وحدة من المقياس يساوي قيمة الوحدة للمقياس المئوي. يبدو أنه من الأنسب كتابة معادلة MKT الأساسية باستخدام درجة الحرارة عند دراسة عمليات الغاز.
العلاقة بين الضغط ودرجة الحرارة
تجريبيًا ، يمكنك التحقق من ذلكتناسب ضغط الغاز مع درجة حرارته. في نفس الوقت وجد أن الضغط يتناسب طرديا مع تركيز الجسيمات:
P=nkT ،
حيث T هي درجة الحرارة المطلقة ، و k ثابت يساوي 1.38 • 10-23J / K.
القيمة الأساسية ، التي لها قيمة ثابتة لجميع الغازات ، تسمى ثابت بولتزمان.
بمقارنة اعتماد الضغط على درجة الحرارة والمعادلة الأساسية لغازات MKT ، يمكننا أن نكتب:
‹Ek ›=3kT: 2
متوسط قيمة الطاقة الحركية لحركة جزيئات الغاز يتناسب مع درجة حرارته. وهذا يعني أن درجة الحرارة يمكن أن تكون بمثابة مقياس للطاقة الحركية لحركة الجسيمات.






