في الرياضيات ، التجميع (يُشار إليه برمز سيجما اليوناني الكبير) هو مجموعة من مجموعات الأرقام. ما هو المبلغ؟ هذه هي نتيجة مثل هذا العمل. إذا تمت إضافة الأرقام واحدة تلو الأخرى من اليسار إلى اليمين ، فإن النتيجة الوسيطة هي مجموع جزئي.
ما هو المبلغ
يمكن أن تكون الأرقام المراد جمعها عددًا صحيحًا أو منطقيًا أو حقيقيًا أو معقدًا. بالإضافة إلى ذلك ، يمكن إضافة أنواع أخرى من القيم: المتجهات والمصفوفات ومتعددة الحدود والعناصر العامة لأي مجموعة مضافة (أو حتى أحادية).
إذا كان عدد عناصر المصطلحات محدودًا ، فإن الجمع يعطي دائمًا قيمة محددة جيدًا. يسمى جمع تسلسل لا نهائي من القيم بالمتسلسلة. يمكن تحديد قيمتها غالبًا باستخدام حد (على الرغم من أن القيمة يمكن أن تكون غير محدودة في بعض الأحيان).
التسلسلات
يمكن تحديد مجموع الأرقام [3 ، 7 ، 2 ، 1] من خلال تعبير قيمته هي مجموع الأرقام المضمنة فيه ، على سبيل المثال 3 + 7 + 2 + 1=13. منذ إضافةبشكل جماعي ، لا يعتمد المجموع على كيفية تجميع المصطلحات ، على سبيل المثال ، (3 + 7) + (2 + 1) و 3 + ((7 + 2) + 1) كلاهما يساوي تسعة ، لذلك عادة ما تكون الأقواس الاستغناء عنها. تعتبر الإضافة أيضًا تبادلية ، لذا فإن إعادة ترتيب المصطلحات لا يغير من قيمة المجموع. لاحظ أن هذه الخاصية قد لا تعمل للتجميع اللانهائي.

لا يوجد تدوين خاص لتلخيص متواليات من هذا النوع. لا يوجد سوى فارق بسيط إذا كان هناك أقل من عنصرين. لا يحتوي جمع تسلسل لعضو واحد على علامة زائد (لا يمكن تمييزه عن شكل الرقم نفسه) ، وإذا لم يكن هناك عناصر على الإطلاق ، فلا يمكن حتى كتابته (ولكن بدلاً من ذلك يمكن الإشارة إليه بواسطة قيمته "0"). ومع ذلك ، إذا تم تحديد شروط التسلسل بواسطة نمط معين ، مثل الوظيفة ، فيمكن أن يكون عامل الجمع مفيدًا أو ضروريًا.
سجل
لفهم ما هو المجموع ، من الضروري أيضًا تحليل مظهره.
لجمع تسلسل من الأعداد الصحيحة من 1 إلى 100 ، غالبًا ما يتم استخدام تعبير يتضمن علامة حذف للإشارة إلى الأعضاء المفقودين: 1 + 2 + 3 + 4 + … + 99 + 100. النمط هو من السهل جدًا رؤيته في هذا المثال. ومع ذلك ، بالنسبة للخيارات الأكثر تعقيدًا ، من الضروري تحديد القاعدة المستخدمة للعثور على قيمة العناصر بالضبط ، والتي يمكن تحقيقها باستخدام عامل الجمع "Σ". باستخدام هذا الرمز (سيغما) ، يمكنك تطبيق الترميز التالي:
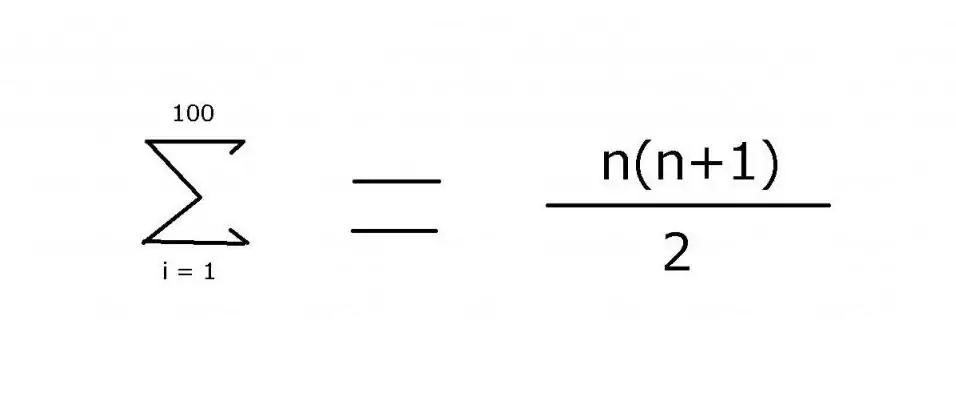
قيمة هذا التعبير هي 5050. يمكن إيجادها باستخدام الاستقراء الرياضي ، حيث جاء الجزء الثاني من الصيغة.
بالنسبة للتسلسلات المختلفة ، ستتغير الصيغة. يتم تقليل عملية التسجيل إلى البحث عن الصورة المسبقة لبعض التسلسل اللانهائي ثم وصفها باستخدام صيغة. بعد القيام بذلك ، ليس من الصعب فهم المبلغ في حالة معينة.
عندما يكون من الضروري توضيح أن الأرقام مضافة مع علاماتها (زائد أو ناقص) ، يتم استخدام المصطلح مجموع جبري. على سبيل المثال ، في نظرية الدائرة الكهربائية ، تأخذ قوانين دائرة كيرشوف بعين الاعتبار المجموع الجبري للتيارات في شبكة الموصلات التي تلتقي عند نقطة معينة ، مما يعطي إشارات معاكسة للتيارات المتدفقة داخل وخارج العقدة.






