في عصرنا ، أصبحت الفيزياء علمًا شائعًا جدًا. إنه موجود حرفيا في كل مكان. المثال الأساسي: تنمو شجرة تفاح في حديقتك ، وتنضج الثمار عليها ، ويحين الوقت ويبدأ التفاح في التساقط ، ولكن في أي اتجاه يسقط؟ بفضل قانون الجاذبية العالمية ، يسقط جنيننا على الأرض ، أي أنه ينخفض ، ولكن ليس لأعلى. لقد كان أحد أشهر أمثلة الفيزياء ، لكن دعونا ننتبه للديناميكا الحرارية ، أو بشكل أكثر دقة ، لتوازن الطور ، الذي لا يقل أهمية في حياتنا.
الديناميكا الحرارية

أولاً ، دعونا نلقي نظرة على هذا المصطلح. ΘερΜοδυναΜική - هكذا تبدو الكلمة في اليونانية. الجزء الأول ΘερΜo يعني "الدفء" ، والجزء الثاني δυναΜική يعني "القوة". الديناميكا الحرارية هي فرع من فروع الفيزياء يدرس خصائص النظام العياني ، بالإضافة إلى الطرق المختلفة لتحويل الطاقة ونقلها. في هذا القسم ، تتم دراسة حالات وعمليات مختلفة بشكل خاص بحيث يمكن إدخال مفهوم درجة الحرارة في الوصف (هذه هي الكمية المادية التي تميز النظام الديناميكي الحراري ويتم قياسها باستخدامبعض الأجهزة). يتم وصف جميع العمليات الجارية في الأنظمة الديناميكية الحرارية فقط بكميات مجهرية (الضغط ودرجة الحرارة ، وكذلك تركيز المكونات).
معادلة Clapeyron-Clausius
يعرف كل فيزيائي هذه المعادلة ، لكن دعونا نقسمها قطعة قطعة. يشير إلى عمليات التوازن لانتقال مادة معينة من مرحلة إلى أخرى. يظهر هذا بوضوح في مثل هذه الأمثلة: الذوبان ، والتبخر ، والتسامي (إحدى طرق الحفاظ على المنتجات ، والتي تحدث عن طريق إزالة الرطوبة تمامًا). توضح الصيغة بوضوح العمليات الجارية:
- n=PV / RT ؛
- حيث T هي درجة حرارة المادة ؛
- ضغط-ف ؛
- حرارة خاصة بـ R لانتقال الطور ؛
- V- تغيير في حجم معين.
تاريخ إنشاء المعادلة

معادلة كلاوزيوس كلابيرون هي تفسير رياضي ممتاز للقانون الثاني للديناميكا الحرارية. يشار إليه أيضًا باسم "عدم المساواة Clausius". وبطبيعة الحال ، تم تطوير النظرية من قبل العالم نفسه ، الذي أراد أن يشرح العلاقة بين تدفق الحرارة في النظام والإنتروبيا ، وكذلك بيئته. تم تطوير هذه المعادلة بواسطة Clausius في محاولاته لشرح وتقدير الانتروبيا. بالمعنى الحرفي ، تمنحنا النظرية الفرصة لتحديد ما إذا كانت العملية الدورية قابلة للعكس أو لا رجوع فيها. تقدم لنا عدم المساواة هذه صيغة كمية لفهم القانون الثاني.
كان العالم من أوائل الذين عملوا على فكرة الانتروبيا ، بل وقدمهااسم العملية. نُشر ما يُعرف الآن باسم نظرية كلاوزيوس لأول مرة في عام 1862 في عمل رودولف السادس ، حول استخدام نظرية التكافؤ التحويلية للعمل الداخلي. حاول العالم إظهار علاقة تناسبية بين الانتروبيا وتدفق الطاقة بالتسخين (δ Q) في النظام. في البناء ، يمكن تحويل هذه الطاقة الحرارية إلى عمل ، ويمكن تحويلها إلى حرارة من خلال عملية دورية. أثبت Rudolph أن "المجموع الجبري لجميع التحويلات التي تحدث في عملية دورية يمكن أن يكون أقل من الصفر أو ، في الحالات القصوى ، يساوي صفرًا".
نظام مغلق معزول
نظام معزول واحد مما يلي:
- النظام المادي بعيد كل البعد عن الآخرين الذين لا يتفاعلون معهم
- يتم إغلاق النظام الديناميكي الحراري بجدران صلبة ثابتة لا يمكن أن تمر من خلالها المادة ولا الطاقة.
على الرغم من حقيقة أن الموضوع مرتبط داخليًا بجاذبيته ، عادةً ما يتم أخذ النظام المعزول إلى ما وراء حدود الجاذبية الخارجية والقوى البعيدة الأخرى.
يمكن أن يتناقض مع ما يسمى (في المصطلحات العامة المستخدمة في الديناميكا الحرارية) بالنظام المغلق المحاط بجدران انتقائية يمكن من خلالها نقل الطاقة على شكل حرارة أو عمل ، ولكن ليس مهمًا. ومع وجود نظام مفتوح تدخل فيه المادة والطاقة أو تخرج منها ، على الرغم من أنها قد تحتوي على العديد من الجدران التي لا يمكن اختراقهاأجزاء من حدودها.
نظام منعزل يخضع لقانون الحفظ. في أغلب الأحيان في الديناميكا الحرارية ، تعتبر المادة والطاقة مفاهيم منفصلة.
التحولات الديناميكية الحرارية
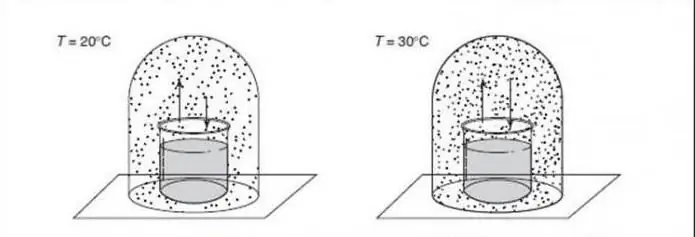
لفهم انتقالات الطور الكمومي ، من المفيد مقارنتها بالتحولات الكلاسيكية (تسمى أيضًا الانقلابات الحرارية). يصف CPT الحافة في الخصائص الديناميكية الحرارية للنظام. يشير إلى إعادة تنظيم الجسيمات. مثال نموذجي هو انتقال الماء المتجمد ، والذي يصف الانتقال السلس بين السائل والصلب. يرجع نمو الطور الكلاسيكي إلى التنافس بين طاقة النظام وانتروبيا التقلبات الحرارية.
لا يحتوي النظام الكلاسيكي على إنتروبيا عند درجة حرارة صفر وبالتالي لا يمكن أن يحدث أي تحول في الطور. يتم تحديد ترتيبها من خلال أول جهد مشتق حراري ديناميكي متقطع. وهي بالطبع من الدرجة الأولى. تحولات الطور من المغناطيس الحديدي إلى البارامغناطيس هي تحويلات مستمرة ومن الدرجة الثانية. يتم وصف هذه التغييرات المستمرة من مرحلة مرتبة إلى مرحلة مضطربة بواسطة معلمة ترتيب تساوي صفرًا. بالنسبة للتحول المغنطيسي الحديدي أعلاه ، ستكون معلمة الطلب هي المغنطة الكلية للنظام.
إمكانات جيبس
طاقة جيبس الحرة هي أقصى قدر من العمل بدون تمدد يمكن إزالته من نظام مغلق بالديناميكا الحرارية (يمكنه تبادل الحرارة والعمل مع البيئة). مثللا يمكن الحصول على النتيجة القصوى إلا في عملية قابلة للعكس تمامًا. عندما يتحول النظام من الحالة الأولى إلى الحالة الثانية ، يكون الانخفاض في طاقة جيبس الحرة مساويًا لتلك التي يؤديها النظام في بيئته ، مطروحًا منه عمل قوى الضغط.
دول التوازن

التوازن الديناميكي الحراري والميكانيكي هو مفهوم بديهي للديناميكا الحرارية. هذه هي الحالة الداخلية لنظام أو أكثر متصلة بجدران نفاذة أو غير منفذة أكثر أو أقل. في هذه الحالة ، لا توجد تدفقات عيانية نقية للمادة أو الطاقة ، سواء داخل نظام أو بين الأنظمة.
في مفهومها الخاص لحالة التوازن الداخلي ، لا يحدث التغيير العياني. الأنظمة في نفس الوقت في توازن حراري ، ميكانيكي ، كيميائي (ثابت) ، إشعاعي. قد يكونون في نفس الشكل. في هذه العملية ، يتم حفظ جميع العروض دفعة واحدة وإلى أجل غير مسمى حتى يتم كسر العملية المادية. في حالة التوازن العياني ، تحدث تبادلات متوازنة دقيقة تمامًا. الدليل أعلاه هو تفسير مادي لهذا المفهوم
أساسيات
لكل قوانين ، نظريات ، صيغ أسسها الخاصة. لنلقِ نظرة على الأسس الثلاثة لقانون توازن الطور
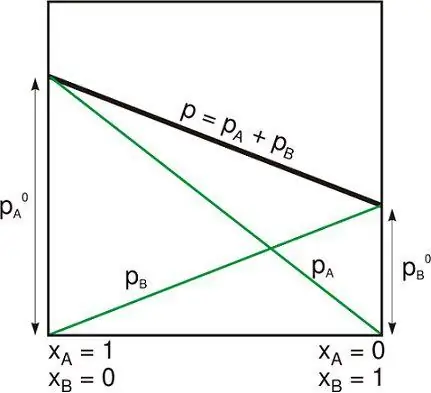
- المرحلة هي شكل من أشكال المادة ، متجانسة في التركيب الكيميائي والحالة الفيزيائية والتوازن الميكانيكي. المراحل النموذجية صلبة وسائلة وغازية.يعتبر سائلين غير قابلين للامتزاج (أو مخاليط سائلة بتركيبات مختلفة) مفصولة بحد منفصل مرحلتين متميزتين ومواد صلبة غير قابلة للامتزاج.
- عدد المكونات (C) هو عدد المكونات المستقلة كيميائيًا للنظام. الحد الأدنى لعدد الأنواع المستقلة المطلوبة لتحديد تكوين جميع مراحل النظام.
- عدد درجات الحرية (F) في هذا السياق هو عدد المتغيرات المكثفة المستقلة عن بعضها البعض.
التصنيف حسب توازن الطور
- تحدث تفاعلات النقل الصافي المستمر (غالبًا ما تسمى تفاعلات الحالة الصلبة) بين مادة صلبة ذات تركيبة مختلفة. قد تشمل العناصر الموجودة في السوائل (H ، C) ، ولكن يتم الاحتفاظ بهذه العناصر في مراحل صلبة ، لذلك لا توجد أطوار سائلة متفاعلة أو منتجات (H2O ، CO2 ). يمكن أن تكون تفاعلات النقل الصلبة النقية مستمرة أو متقطعة أو نهائية.
- متعدد الأشكال هو نوع خاص من تفاعل الطور الصلب الذي يتضمن مراحل من التركيب المتطابق. الأمثلة الكلاسيكية هي التفاعلات بين سيليكات الألومنيوم كيانيت-سيليمانايت-أندالوسيت ، وتحويل الجرافيت إلى الماس عند الضغط العالي ، وتوازن كربونات الكالسيوم.
قوانين التوازن

اقترح يوشيا ويلارد جيبس قاعدة مصنع جيبس في ورقته الشهيرة بعنوان "توازن المواد غير المتجانسة" ، والتي ظهرت من عام 1875 إلى عام 1878. ينطبق علىأنظمة غير متجانسة متعددة المكونات غير تفاعلية في توازن ديناميكي حراري وهي مساواة معينة:
- F=C-P + 2 ؛
- حيث F هو عدد درجات الحرية ؛
- C - عدد المكونات ؛
- P - عدد المراحل في التوازن الديناميكي الحراري مع بعضها البعض.
عدد درجات الحرية هو عدد المتغيرات المكثفة غير المشغولة. أكبر عدد من المعلمات الديناميكية الحرارية ، مثل درجة الحرارة أو الضغط ، التي يمكن أن تختلف بشكل متزامن وتعسفي دون التأثير على بعضها البعض. مثال على نظام مكون واحد هو واحد يحتوي على مادة كيميائية نقية واحدة ، في حين أن الأنظمة المكونة من عنصرين ، مثل خلائط الماء والإيثانول ، لها مكونان مستقلان. انتقالات الطور النموذجية (توازن الطور) هي المواد الصلبة والسوائل والغازات.
حكم الطور عند الضغط المستمر
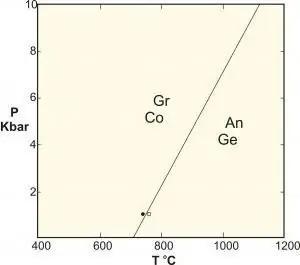
للتطبيقات في علم المواد التي تتعامل مع تغيرات الطور بين الهياكل الصلبة المختلفة ، غالبًا ما يحدث ضغط ثابت (مثل جو واحد) ويتم تجاهله كدرجة من الحرية ، لذلك تصبح القاعدة: F=C - P + 1
يتم تقديم هذه الصيغة أحيانًا تحت اسم "قاعدة المرحلة المكثفة" ، ولكن كما نعلم ، لا تنطبق على هذه الأنظمة التي تخضع لضغوط عالية (على سبيل المثال ، في الجيولوجيا) ، نظرًا لعواقب هذه يمكن أن تسبب الضغوط عواقب وخيمة.
قد يبدو أن توازن الطور هو مجرد عبارة فارغة ، وهناك القليل من العمليات الفيزيائية التي تكون فيها هذه اللحظةمتورط ، ولكن ، كما رأينا ، بدونها ، العديد من القوانين التي نعرفها لا تعمل ، لذلك تحتاج إلى التعرف قليلاً على هذه القواعد الفريدة والملونة ، وإن كانت مملة بعض الشيء. ساعدت هذه المعرفة الكثير من الناس. لقد تعلموا كيفية تطبيقها على أنفسهم ، على سبيل المثال ، يمكن للكهربائيين ، الذين يعرفون قواعد العمل بالمراحل ، حماية أنفسهم من الخطر غير الضروري.






