قسم مهم من الديناميكا الحرارية هو دراسة التحولات بين المراحل المختلفة للمادة ، لأن هذه العمليات تحدث في الممارسة العملية ولها أهمية أساسية للتنبؤ بسلوك نظام في ظل ظروف معينة. تسمى هذه التحولات انتقالات الطور ، والتي تم تخصيص المقالة لها.
مفهوم المرحلة ومكون النظام

قبل الشروع في النظر في انتقالات الطور في الفيزياء ، من الضروري تحديد مفهوم المرحلة نفسها. كما هو معروف من مسار الفيزياء العامة ، هناك ثلاث حالات للمادة: الغازية والصلبة والسائلة. في قسم خاص من العلوم - في الديناميكا الحرارية - تتم صياغة القوانين لمراحل المادة ، وليس لحالات تجميعها. يُفهم الطور على أنه حجم معين من المادة له بنية متجانسة ، ويتميز بخصائص فيزيائية وكيميائية محددة ويتم فصله عن بقية المادة بواسطة حدود تسمى الطور البيني.
وهكذا ، يحمل مفهوم "المرحلة" معلومات أكثر أهمية من الناحية العملية حول الخصائصمسألة من حالتها التجميعية. على سبيل المثال ، يمكن أن تكون الحالة الصلبة لمعدن مثل الحديد في المراحل التالية: مكعب مغناطيسي منخفض الحرارة متمركز حول الجسم (BCC) ، ومكعب ذو درجة حرارة منخفضة غير مغناطيسي ، ومكعب محوره الوجه (fcc) ، ومكعب عالي درجة الحرارة غير المغناطيسية bcc.
بالإضافة إلى مفهوم "الطور" ، تستخدم قوانين الديناميكا الحرارية أيضًا مصطلح "المكونات" ، وهو ما يعني عدد العناصر الكيميائية التي تشكل نظامًا معينًا. هذا يعني أن المرحلة يمكن أن تكون إما أحادية المكون (عنصر كيميائي واحد) أو متعددة المكونات (عدة عناصر كيميائية).
نظرية جيبس والتوازن بين مراحل النظام

لفهم انتقالات الطور ، من الضروري معرفة شروط التوازن بينها. يمكن الحصول على هذه الشروط رياضيًا عن طريق حل نظام معادلات جيبس لكل منها ، بافتراض الوصول إلى حالة التوازن عندما تتوقف طاقة جيبس الإجمالية للنظام المعزول عن التأثير الخارجي عن التغيير.
نتيجة لحل نظام المعادلات المشار إليه ، يتم الحصول على شروط لوجود توازن بين عدة مراحل: سيتوقف النظام المعزول عن التطور فقط عندما تكون الضغوط والإمكانات الكيميائية لكل مكون ودرجات الحرارة في جميع المراحل متساوية مع بعضها البعض
قاعدة طور جيبس للتوازن

يمكن أن يكون النظام الذي يتكون من عدة مراحل ومكونات في حالة توازن ليس فقطتحت ظروف معينة ، على سبيل المثال ، عند درجة حرارة وضغط معينين. يمكن تغيير بعض المتغيرات في نظرية جيبس للتوازن مع الحفاظ على كل من عدد المراحل وعدد المكونات الموجودة في هذا التوازن. عدد المتغيرات التي يمكن تغييرها دون الإخلال بالتوازن في النظام يسمى عدد الحريات لهذا النظام.
يتم تحديد عدد الحريات l لنظام يتكون من مكونات f و k بشكل فريد من قاعدة مرحلة Gibbs. تتم كتابة هذه القاعدة رياضيًا على النحو التالي: l + f=k + 2. كيف تتعامل مع هذه القاعدة؟ بسيط جدا. على سبيل المثال ، من المعروف أن النظام يتكون من f=3 مراحل توازن. ما هو الحد الأدنى لعدد المكونات التي يمكن أن يحتويها مثل هذا النظام؟ يمكنك الإجابة على السؤال من خلال التفكير على النحو التالي: في حالة التوازن ، توجد أكثر الشروط صرامة عندما يتم إدراكها فقط عند مؤشرات معينة ، أي أن التغيير في أي معلمة ديناميكية حرارية سيؤدي إلى عدم التوازن. هذا يعني أن عدد الحريات l=0. باستبدال القيم المعروفة لـ l و f ، نحصل على k=1 ، أي أن النظام الذي توجد فيه ثلاث مراحل في حالة توازن يمكن أن يتكون من مكون واحد. المثال الرئيسي هو النقطة الثلاثية للماء ، حيث يوجد الجليد والماء السائل والبخار في حالة توازن عند درجات حرارة وضغوط محددة.
تصنيف تحولات الطور
إذا بدأت في تغيير بعض المعلمات الديناميكية الحرارية في نظام في حالة توازن ، يمكنك ملاحظة كيف ستختفي مرحلة ما وستظهر مرحلة أخرى. مثال بسيط على هذه العملية هو ذوبان الجليد عند تسخينه.
نظرًا لأن معادلة جيبس تعتمد فقط على متغيرين (الضغط ودرجة الحرارة) ، وأن انتقال الطور يتضمن تغييرًا في هذه المتغيرات ، فيمكن وصف الانتقال بين المراحل رياضيًا عن طريق التفريق بين طاقة جيبس فيما يتعلق بها المتغيرات. كان هذا هو النهج الذي استخدمه الفيزيائي النمساوي Paul Ehrenfest في عام 1933 ، عندما قام بتجميع تصنيف لجميع العمليات الديناميكية الحرارية المعروفة التي تحدث مع تغيير في توازن الطور.
من أساسيات الديناميكا الحرارية ، يترتب على ذلك أن المشتق الأول لطاقة جيبس فيما يتعلق بدرجة الحرارة يساوي التغير في إنتروبيا النظام. مشتق طاقة جيبس فيما يتعلق بالضغط يساوي التغير في الحجم. إذا ، عندما تتغير مراحل النظام ، فإن الانتروبيا أو الحجم تعاني من انقطاع ، أي أنها تتغير فجأة ، ثم يتحدثون عن انتقال طور من الدرجة الأولى.
علاوة على ذلك ، فإن المشتقات الثانية لطاقة جيبس فيما يتعلق بدرجة الحرارة والضغط هي السعة الحرارية ومعامل التمدد الحجمي ، على التوالي. إذا كان التحول بين المراحل مصحوبًا بانقطاع في قيم الكميات المادية المشار إليها ، فعندئذٍ يتحدث المرء عن انتقال طور من الدرجة الثانية.
أمثلة على التحولات بين المراحل

هناك عدد كبير من التحولات المختلفة في الطبيعة. في إطار هذا التصنيف ، من الأمثلة البارزة على التحولات من النوع الأول عمليات صهر المعادن أو تكثيف بخار الماء من الهواء ، عندما يكون هناك قفزة في الحجم في النظام.
إذا تحدثنا عن انتقالات الدرجة الثانية ، فإن الأمثلة اللافتة للنظر هي تحول الحديد من حالة مغناطيسية إلى حالة بارامغناطيسية عند درجة حرارة768 درجة مئوية أو تحول موصل معدني إلى حالة فائقة التوصيل عند درجات حرارة قريبة من الصفر المطلق.
المعادلات التي تصف انتقالات من النوع الأول
من الناحية العملية ، غالبًا ما يكون من الضروري معرفة كيفية تغير درجة الحرارة والضغط والطاقة الممتصة (المنبعثة) في النظام عندما تحدث تحولات الطور فيه. يتم استخدام معادلتين مهمتين لهذا الغرض. يتم الحصول عليها بناءً على معرفة أساسيات الديناميكا الحرارية:
- صيغة Clapeyron ، التي تؤسس العلاقة بين الضغط ودرجة الحرارة أثناء التحولات بين المراحل المختلفة.
- صيغة Clausius التي تربط الطاقة الممتصة (المحررة) ودرجة حرارة النظام أثناء التحول.
استخدام كلتا المعادلتين ليس فقط في الحصول على التبعيات الكمية للكميات المادية ، ولكن أيضًا في تحديد علامة منحدر منحنيات التوازن على مخططات الطور.
معادلة لوصف انتقالات من النوع الثاني

انتقالات الطور من النوع الأول والثاني موصوفة بمعادلات مختلفة ، لأن تطبيق معادلات كلاوسيوس وكلاوسيوس للانتقالات من الدرجة الثانية يؤدي إلى عدم اليقين الرياضي.
لوصف هذا الأخير ، يتم استخدام معادلات إهرنفست ، والتي تؤسس علاقة بين التغيرات في الضغط ودرجة الحرارة من خلال معرفة التغيرات في السعة الحرارية ومعامل التمدد الحجمي أثناء عملية التحول. تُستخدم معادلات إهرنفست لوصف انتقالات الموصل الفائق في حالة عدم وجود مجال مغناطيسي.
الأهميةمخططات المرحلة
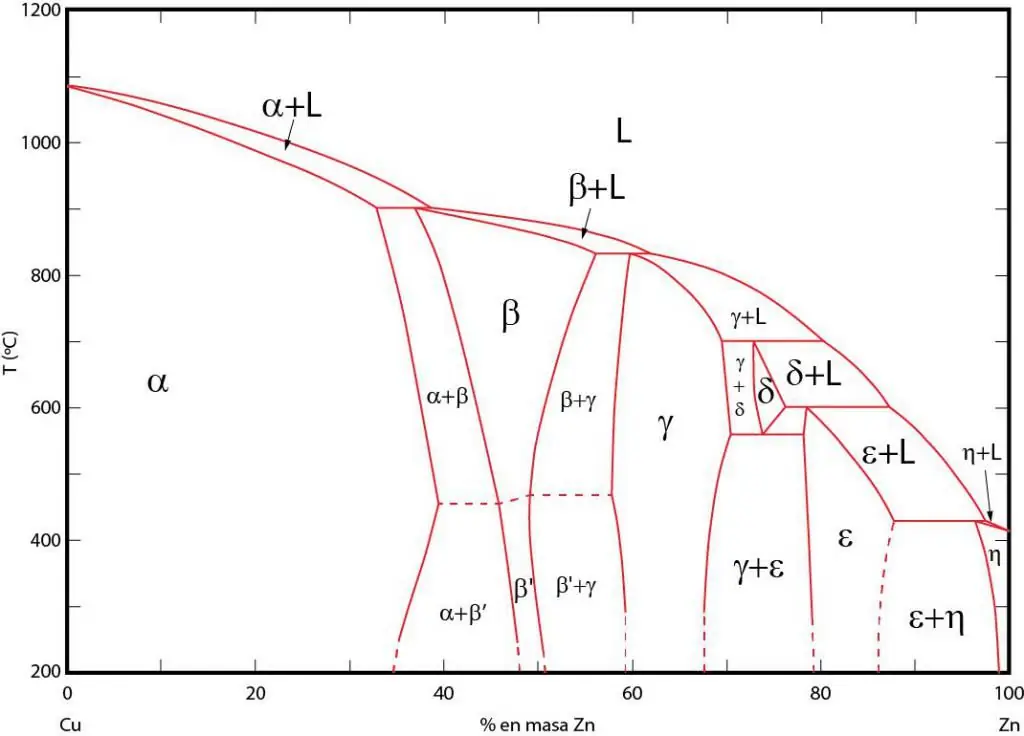
مخططات الطور هي تمثيل رسومي للمناطق التي توجد فيها المراحل المقابلة في حالة توازن. يتم فصل هذه المناطق بخطوط التوازن بين المراحل. غالبًا ما تستخدم مخططات الطور P-T (درجة حرارة الضغط) و T-V (درجة الحرارة-الحجم) و P-V (حجم الضغط).
تكمن أهمية مخططات الطور في حقيقة أنها تسمح لك بالتنبؤ بالمرحلة التي سيكون فيها النظام عندما تتغير الظروف الخارجية وفقًا لذلك. يتم استخدام هذه المعلومات في المعالجة الحرارية للمواد المختلفة من أجل الحصول على هيكل بالخصائص المرغوبة.






