في الفيزياء ، تتم دراسة موضوع الاتصال المتوازي والمتسلسل ، ولا يمكن أن يكون الموصلات فقط ، ولكن أيضًا المكثفات. من المهم هنا عدم الخلط بين الكيفية التي يبدو بها كل منهم في الرسم التخطيطي. وعندها فقط قم بتطبيق صيغ محددة. بالمناسبة ، عليك أن تتذكرها عن ظهر قلب.
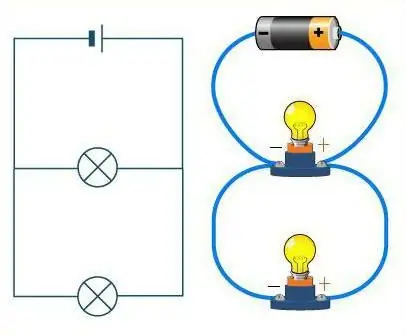
كيف نميز بين هذين المركبين
ألق نظرة فاحصة على الرسم التخطيطي. إذا تم تمثيل الأسلاك كطريق ، فإن السيارات الموجودة عليها ستلعب دور المقاومات. على طريق مستقيم بدون مفترقات ، تسير السيارات واحدة تلو الأخرى في سلسلة. يبدو أيضًا أن توصيل سلسلة الموصلات هو نفسه. يمكن أن يحتوي الطريق في هذه الحالة على عدد غير محدود من المنعطفات ، ولكن ليس تقاطعًا واحدًا. بغض النظر عن كيفية اهتزاز الطريق (الأسلاك) ، ستظل الآلات (المقاومات) موجودة دائمًا واحدة تلو الأخرى ، في سلسلة واحدة.
إنها مسألة مختلفة تمامًا إذا تم النظر في اتصال متوازي. ثم يمكن مقارنة المقاومات بالرياضيين في البداية. هم انهمكل يقف على مساره الخاص ، لكن لهما نفس اتجاه الحركة ، وخط النهاية في نفس المكان. وبالمثل ، فإن المقاومات - لكل منها سلك خاص بها ، لكنها كلها متصلة ببعضها البعض.
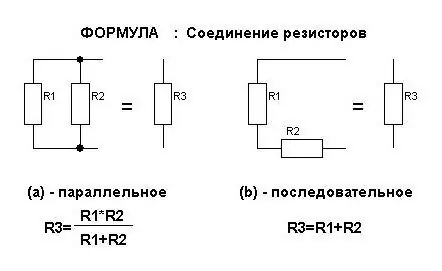
صيغ للقوة الحالية
دائما يناقش في موضوع "الكهرباء". تؤثر التوصيلات المتوازية والمتسلسلة على مقدار التيار في المقاومات بطرق مختلفة. بالنسبة لهم ، يتم اشتقاق الصيغ التي يمكن تذكرها. لكن يكفي فقط أن نتذكر المعنى الذي تم استثماره فيهم.
إذن ، التيار في سلسلة توصيل الموصلات هو نفسه دائمًا. أي أن قيمة القوة الحالية في كل منها لا تختلف. يمكنك رسم تشبيه إذا قارنت سلكًا بأنبوب. في ذلك ، يتدفق الماء دائمًا بنفس الطريقة. وكل العوائق التي تعترض طريقها ستزول بنفس القوة. نفس الشيء مع التيار. لذلك ، فإن صيغة إجمالي التيار في دائرة متصلة بسلسلة من المقاومات تبدو كما يلي:
Igen=أنا1=أنا2
هنا الحرف الأول يدل على قوة التيار. هذا تدوين شائع ، لذلك عليك أن تتذكره.
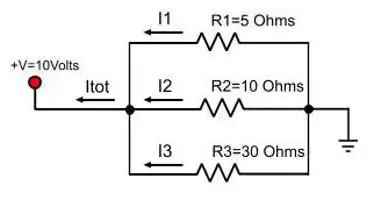
لن يكون التيار في الاتصال المتوازي قيمة ثابتة بعد الآن. بنفس القياس مع الأنبوب ، اتضح أن الماء سيقسم إلى مجريين إذا كان للأنبوب الرئيسي فرع. تُلاحظ نفس الظاهرة مع التيار عندما يظهر فرع من الأسلاك في مساره. معادلة إجمالي القوة الحالية عند توصيل الموصلات بالتوازي:
أناgen=أنا1+ أنا2
إذا كان المتفرعة مكونة من الأسلاك ذلكأكثر من اثنين ، ثم في الصيغة أعلاه سيكون هناك المزيد من المصطلحات بنفس الرقم.
صيغ للتوتر
عندما يتم النظر في الدائرة التي يتم فيها توصيل الموصلات في سلسلة ، يتم تحديد الجهد في القسم بأكمله من خلال مجموع هذه القيم على كل مقاوم محدد. يمكنك مقارنة هذه الحالة باللوحات. سيكون من السهل على شخص واحد أن يمسك بأحدهم ، كما أنه سيكون قادرًا على أخذ الثاني القريب ، ولكن بصعوبة. لن يتمكن شخص واحد بعد الآن من حمل ثلاث لوحات بجانب بعضها البعض ، وستكون هناك حاجة إلى مساعدة ثانية. إلخ. جهود الناس تتضافر.
معادلة الجهد الكلي لجزء من الدائرة مع توصيل سلسلة من الموصلات تبدو كما يلي:
Ugen=U1+ U2، حيث U هي التسمية المعتمدة للجهد الكهربائي
ينشأ موقف آخر إذا تم النظر في اتصال موازٍ للمقاومات. عندما يتم تكديس الأطباق فوق بعضها البعض ، فلا يزال بإمكان شخص واحد حملها. لذلك ليس عليك إضافة أي شيء. لوحظ نفس القياس عندما تكون الموصلات متصلة بالتوازي. الجهد على كل منهم هو نفسه ويساوي ذلك الموجود عليهم جميعًا مرة واحدة. صيغة الجهد الكلي هي:
Ugen=U1=U2
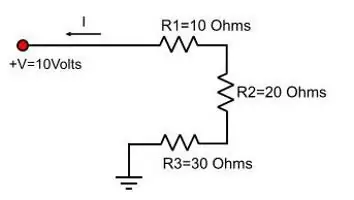
صيغ المقاومة الكهربائية
لم يعد بإمكانك حفظها ، لكن تعرف معادلة قانون أوم واشتق منها ما تريد. ويترتب على هذا القانون أنالجهد يساوي ناتج التيار والمقاومة. أي U=IR حيث R هي المقاومة
ثم تعتمد الصيغة التي ستحتاج إلى العمل معها على كيفية توصيل الموصلات:
- في السلسلة ، لذا فأنت بحاجة إلى المساواة في الجهد - أناالجنرال Rالمجموع=أنا1 R1+ أنا2 R2 ؛
- بالتوازي ، من الضروري استخدام صيغة القوة الحالية - Utotal/ Rtotal=U 1/ R1+ U2/ R2.
متبوعة بتحولات بسيطة ، والتي تستند إلى حقيقة أن جميع التيارات لها نفس القيمة في المساواة الأولى ، وفي الثانية - الفولتية متساوية. حتى يمكن تقصيرها. أي ، يتم الحصول على التعبيرات التالية:
- Rgen=R1+ R2(للتوصيل المتسلسل للموصلات)
- 1 / Rgen=1 / R1+ 1 / R2(عند التوصيل بالتوازي).
عندما يزداد عدد المقاومات المتصلة بالشبكة ، يتغير عدد المصطلحات في هذه التعبيرات.
تجدر الإشارة إلى أن الاتصال المتوازي والمتسلسل للموصلات له تأثير مختلف على المقاومة الكلية. أولهم يقلل من مقاومة قسم الدائرة. علاوة على ذلك ، اتضح أنه أقل من أصغر المقاومات المستخدمة. عند الاتصال في سلسلة ، يكون كل شيء منطقيًا: القيم تتراكم ، لذا سيكون العدد الإجمالي دائمًا هو الأكبر.
العمل الحالي
تشكل الكميات الثلاثة السابقة قوانين التوصيل المتوازي والترتيب المتسلسل للموصلات في الدائرة. لذلك ، لا بد من معرفتهم. حول العمل والقوة ، ما عليك سوى أن تتذكر الصيغة الأساسية. هو مكتوب على النحو التالي: A \u003d IUt ، حيث A هو عمل التيار ، t هو وقت مروره عبر الموصل.
من أجل تحديد إجمالي العمل باتصال تسلسلي ، تحتاج إلى استبدال الجهد في التعبير الأصلي. تحصل على المساواة: A \u003d I(U1+ U2)t ، فتح الأقواس التي تبين أن العمل على القسم بأكمله يساوي مقدارها على كل مستهلك حالي محدد.
يستمر التفكير بشكل مشابه إذا تم النظر في مخطط اتصال متوازي. من المفترض أن يتم استبدال القوة الحالية فقط. لكن النتيجة ستكون هي نفسها: A=A1+ A2.
القوة الحالية
عند اشتقاق صيغة للطاقة (تدوين "P") لقسم الدائرة ، تحتاج مرة أخرى إلى استخدام صيغة واحدة: P \u003d UI. بعد هذا المنطق ، اتضح أن الاتصالات المتوازية والمتسلسلة هي موصوفة بهذه الصيغة للسلطة: P \u003d P1+ P2.
أي بغض النظر عن كيفية وضع المخططات ، فإن القوة الإجمالية ستكون مجموع المشاركين في العمل. هذا يفسر حقيقة أنه من المستحيل تضمين العديد من الأجهزة القوية في شبكة الشقة في نفس الوقت. هي فقط لا تستطيع تحمل العبء
كيف يؤثر توصيل الموصلات على إصلاح إكليل رأس السنة الجديدة؟
مباشرة بعد أن تحترق إحدى المصابيح ، يتضح كيف تم توصيلها. فياتصال تسلسلي ، لن يضيء أي منهم. ويرجع ذلك إلى حقيقة أن المصباح الذي أصبح غير قابل للاستخدام يتسبب في حدوث انقطاع في الدائرة. لذلك ، تحتاج إلى التحقق من كل شيء لتحديد أي واحد تم حرقه واستبداله - وسيبدأ الطوق في العمل.
إذا كان يستخدم اتصالاً متوازيًا ، فلن يتوقف عن العمل إذا فشل أحد المصابيح. بعد كل شيء ، لن تنكسر السلسلة تمامًا ، بل جزء واحد موازٍ فقط. لإصلاح مثل هذا الطوق ، لا تحتاج إلى فحص جميع عناصر الدائرة ، ولكن فقط العناصر التي لا تتوهج.
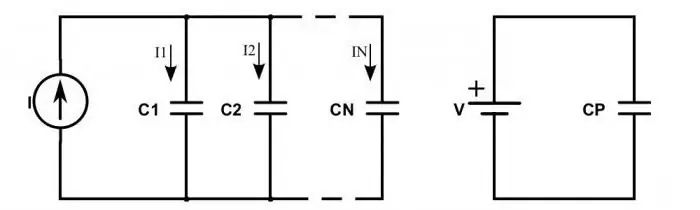
ماذا يحدث للدائرة إذا تم تضمين المكثفات بدلاً من المقاومات؟
عندما يتم توصيلها في سلسلة ، يتم ملاحظة الموقف التالي: الشحنات من إيجابيات مصدر الطاقة تأتي فقط إلى الصفائح الخارجية للمكثفات المتطرفة. أولئك الموجودون في المنتصف يمررون تلك الشحنة على طول السلسلة. وهذا ما يفسر حقيقة ظهور نفس الشحنات على جميع اللوحات ، ولكن بعلامات مختلفة. لذلك ، يمكن كتابة الشحنة الكهربائية لكل مكثف متصل في سلسلة على النحو التالي:
qgen=q1=q2.
من أجل تحديد الجهد على كل مكثف ، سوف تحتاج إلى معرفة الصيغة: U=q / C. في ذلك ، C هي سعة المكثف.
يتبع إجمالي الجهد نفس قانون المقاومات. لذلك ، عند استبدال الجهد في صيغة السعة بالمجموع ، نحصل على أنه يجب حساب السعة الإجمالية للأجهزة باستخدام الصيغة:
C=q / (U1+ U 2).
يمكنك تبسيط هذه الصيغة عن طريق قلب الكسور واستبدال نسبة الجهد إلى الشحن بالسعة. اتضح المساواة التالية: 1 / С=1 / С1+ 1 / С2.
يبدو الوضع مختلفًا نوعًا ما عند توصيل المكثفات بشكل متوازٍ. ثم يتم تحديد الشحنة الإجمالية من خلال مجموع كل الرسوم التي تتراكم على لوحات جميع الأجهزة. ولا تزال قيمة الجهد تحدد وفقًا للقوانين العامة. لذلك ، فإن صيغة السعة الكلية للمكثفات المتصلة بالتوازي هي:
С=(q 1 + q 2) / U.
أي أن هذه القيمة تعتبر مجموع كل من الأجهزة المستخدمة في الاتصال:
S=S1+ S2.
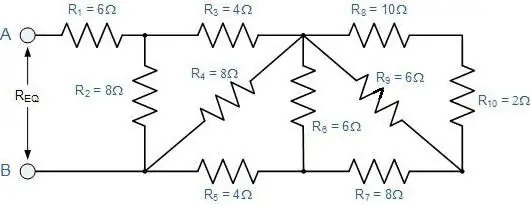
كيفية تحديد المقاومة الكلية لوصلة عشوائية من الموصلات؟
أي القسم الذي تحل فيه الأقسام المتعاقبة محل الأقسام المتوازية ، والعكس صحيح. بالنسبة لهم ، لا تزال جميع القوانين الموصوفة سارية. ما عليك سوى تطبيقها على مراحل.
أولاً ، من المفترض أن يوسع المخطط عقلياً. إذا كان من الصعب تخيل ذلك ، فأنت بحاجة إلى رسم ما يحدث. سيصبح الشرح أكثر وضوحا إذا نظرنا إليه بمثال محدد (انظر الشكل).
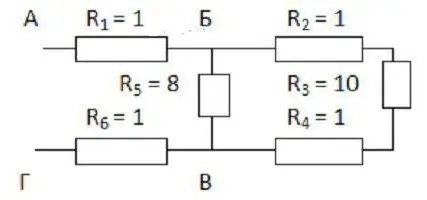
من الملائم البدء في الرسم من النقطتين B و C. يجب وضعها على مسافة ما من بعضها البعض ومن حواف الورقة. على اليسار ، يقترب سلك واحد من النقطة B ، وسلكان موجهان بالفعل إلى اليمين. من ناحية أخرى ، للنقطة B فرعين على اليسار ، وسلك واحد بعدها.
الآن أنت بحاجة لملء الفراغ بين هذهالنقاط. يجب وضع ثلاثة مقاومات ذات معاملات 2 و 3 و 4 على طول السلك العلوي ، والمقاوم الذي يحتوي على فهرس 5 سينطلق من الأسفل ، ويتم توصيل المقاومات الثلاثة الأولى في سلسلة. مع المقاوم الخامس هم على التوازي.
المقاومات المتبقية (الأولى والسادسة) متصلة في سلسلة مع القسم المدروس من BV. لذلك ، يمكن ببساطة استكمال الرسم بمستطيلين على جانبي النقاط المحددة. يبقى تطبيق الصيغ لحساب المقاومة:
- الأول المعطى للاتصال التسلسلي ؛
- ثم للتوازي ؛
- ومرة أخرى على التوالي.
بهذه الطريقة ، يمكنك نشر أي مخطط ، حتى معقد للغاية.
مشكلة التوصيل التسلسلي للموصلات
الحالة. مصباحان ومقاوم متصلان في دائرة أحدهما خلف الآخر. الجهد الإجمالي 110 فولت والتيار 12 أ. ما قيمة المقاوم إذا كان كل مصباح مصنّفًا عند 40 فولت؟
القرار. نظرًا لأنه يتم النظر في اتصال سلسلة ، فإن الصيغ لقوانينها معروفة. تحتاج فقط إلى تطبيقها بشكل صحيح. ابدأ بمعرفة قيمة الجهد عبر المقاوم. للقيام بذلك ، تحتاج إلى طرح ضعف جهد مصباح واحد من الإجمالي. اتضح 30 V.
الآن بعد أن عُرفت كميتان ، U و I (تم إعطاء الثانية منهما في الحالة ، نظرًا لأن إجمالي التيار يساوي التيار في كل مستهلك سلسلة) ، يمكننا حساب مقاومة المقاوم باستخدام قانون أوم. اتضح أن 2.5 أوم.
إجابة. مقاومة المقاوم 2.5 اوم
مهمةلتوصيل المكثفات المتوازية والمتسلسلة
الحالة. توجد ثلاث مكثفات بسعات 20 و 25 و 30 ميكروفاراد. حدد السعة الكلية عند التوصيل على التوالي وعلى التوازي.
القرار. من الأسهل أن تبدأ باتصال متوازي. في هذه الحالة ، يجب إضافة جميع القيم الثلاث فقط. وبالتالي ، فإن السعة الإجمالية 75 فائق التوهج.
ستكون الحسابات أكثر تعقيدًا إلى حد ما عندما يتم توصيل هذه المكثفات في سلسلة. بعد كل شيء ، تحتاج أولاً إلى إيجاد نسبة الوحدة لكل من هذه القدرات ، ثم إضافتها إلى بعضها البعض. اتضح أن الوحدة مقسومة على السعة الإجمالية 37/300. ثم القيمة المطلوبة ما يقرب من 8 ميكروفاراد.
إجابة. السعة الكلية في سلسلة التوصيل هي 8 uF ، بالتوازي - 75 uF.






