يواجه كل شخص خلال حياته أجسادًا في إحدى الحالات الثلاث الكلية للمادة. أبسط حالة تجميع للدراسة هي الغاز. في المقال ، سننظر في مفهوم الغاز المثالي ، ونعطي معادلة حالة النظام ، وكذلك نولي بعض الاهتمام لوصف درجة الحرارة المطلقة.
حالة الغاز
لدى كل طالب فكرة جيدة عن حالة المادة التي يتحدثون عنها عندما يسمعون كلمة "غاز". تُفهم هذه الكلمة على أنها جسد قادر على احتلال أي حجم يتم توفيره لها. إنها غير قادرة على الحفاظ على شكلها ، لأنها لا تستطيع أن تقاوم حتى أدنى تأثير خارجي. كما أن الغاز لا يحتفظ بالحجم مما يميزه ليس فقط عن المواد الصلبة ولكن أيضًا عن السوائل.
الغاز هو مادة سائلة مثل السائل. في عملية حركة الأجسام الصلبة في الغازات ، فإن الأخير يعيق هذه الحركة. القوة الناتجة تسمى المقاومة. تعتمد قيمتها علىسرعة الجسم في الغاز
الأمثلة القوية للغازات هي الهواء والغاز الطبيعي المستخدم لتدفئة المنازل والطهي والغازات الخاملة (Ne ، Ar) المستخدمة لملء أنابيب التوهج الإعلانية أو المستخدمة لإنشاء بيئة خاملة (غير عدوانية ووقائية) عند اللحام
الغاز المثالي
قبل الشروع في وصف قوانين الغاز ومعادلة الحالة ، يجب أن تفهم جيدًا السؤال عن ماهية الغاز المثالي. تم تقديم هذا المفهوم في النظرية الحركية الجزيئية (MKT). الغاز المثالي هو أي غاز تتوفر فيه الخصائص التالية:
- الجسيمات التي تشكلها لا تتفاعل مع بعضها البعض باستثناء الاصطدامات الميكانيكية المباشرة.
- نتيجة اصطدام الجسيمات بجدران الوعاء أو فيما بينها ، يتم الحفاظ على طاقتها الحركية وزخمها ، أي أن الاصطدام يعتبر مرنًا تمامًا.
- الجسيمات ليس لها أبعاد ، ولكن لها كتلة محدودة ، أي أنها تشبه النقاط المادية.
من الطبيعي ألا يكون أي غاز مثاليًا ولكنه حقيقي. ومع ذلك ، لحل العديد من المشاكل العملية ، هذه التقريبات صالحة تمامًا ويمكن استخدامها. هناك قاعدة تجريبية عامة تقول: بغض النظر عن الطبيعة الكيميائية ، إذا كان للغاز درجة حرارة أعلى من درجة حرارة الغرفة وضغطًا بترتيب الغلاف الجوي أو أقل ، فيمكن اعتباره مثاليًا بدقة عالية ويمكن استخدامه لوصف هو - هي.صيغة معادلة الغاز المثالية للدولة
قانون كلابيرون مينديليف
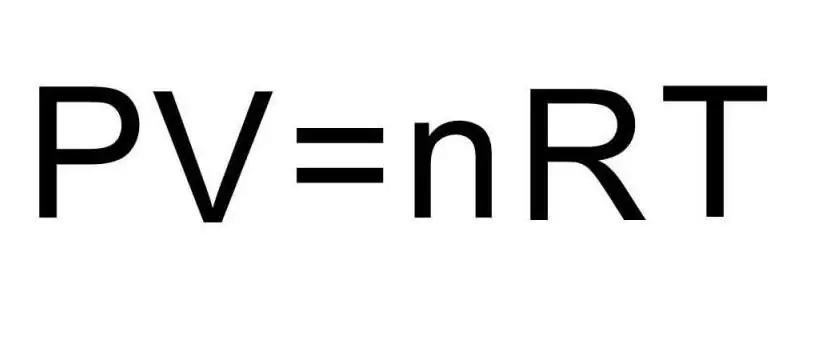
يتم التعامل مع التحولات بين الحالات التجميعية المختلفة للمادة والعمليات داخل حالة تجميعية واحدة بواسطة الديناميكا الحرارية. الضغط ودرجة الحرارة والحجم هي ثلاث كميات تحدد بشكل فريد أي حالة للنظام الحراري الديناميكي. تجمع صيغة معادلة حالة الغاز المثالي بين هذه الكميات الثلاثة في مساواة واحدة. لنكتب هذه الصيغة:
PV=nRT
هنا P ، V ، T - الضغط والحجم ودرجة الحرارة ، على التوالي. قيمة n هي كمية المادة في المولات ، والرمز R يشير إلى الثابت العام للغازات. توضح هذه المساواة أنه كلما زاد ناتج الضغط والحجم ، يجب أن يكون ناتج كمية المادة ودرجة الحرارة أكبر.

تسمى صيغة معادلة حالة الغاز قانون Clapeyron-Mendeleev. في عام 1834 ، توصل العالم الفرنسي إميل كلابيرون إلى هذه المعادلة ، لخصًا النتائج التجريبية لأسلافه. ومع ذلك ، استخدم كلابيرون عددًا من الثوابت ، والتي استبدلها مندليف لاحقًا بواحد - ثابت الغاز العام R (8 ، 314 J / (molK)). لذلك سميت هذه المعادلة في الفيزياء الحديثة على اسم علماء فرنسيين وروس.

أشكال المعادلات الأخرى
أعلاه ، كتبنا معادلة مندليف-كلابيرون للحالة للغاز المثالي في المعادلة المقبولة عمومًا وشكل مناسب. ومع ذلك ، في مشاكل الديناميكا الحرارية ، غالبًا ما تكون هناك حاجة إلى شكل مختلف قليلاً. تمت كتابة ثلاث صيغ أخرى أدناه ، والتي تتبع مباشرة من المعادلة المكتوبة:
PV=NkB T ؛
PV=م / مRT ؛
P=ρRT / M.
هذه المعادلات الثلاث هي أيضًا عالمية للغاز المثالي ، وتظهر فيها فقط كميات مثل الكتلة م والكتلة المولية M والكثافة ρ وعدد الجسيمات N التي يتكون منها النظام. يشير الرمز kBهنا إلى ثابت Boltzmann (1 ، 3810-23J / K).
قانون بويل ماريوت
عندما صاغ كلابيرون معادلته ، كان يعتمد على قوانين الغاز التي تم اكتشافها تجريبياً قبل عدة عقود. أحدها هو قانون بويل ماريوت. إنه يعكس عملية متساوية الحرارة في نظام مغلق ، ونتيجة لذلك تتغير المعلمات العيانية مثل الضغط والحجم. إذا وضعنا ثابت T و n في معادلة الحالة للغاز المثالي ، فسيأخذ قانون الغاز الشكل التالي:
P1 V1=P2 V2
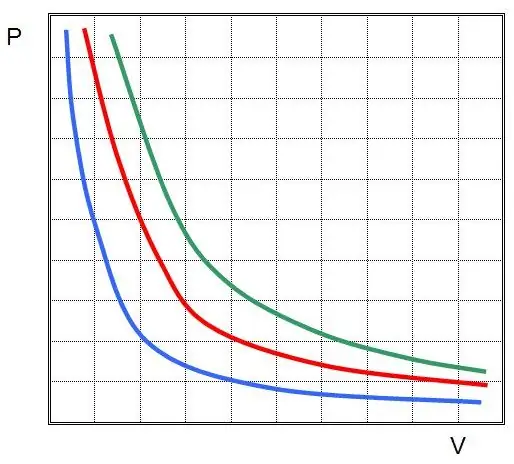
هذا هو قانون Boyle-Mariotte ، الذي ينص على الحفاظ على ناتج الضغط والحجم أثناء عملية متساوية الحرارة. في هذه الحالة ، تتغير القيمتان P و V نفسيهما.
إذا قمت برسم P (V) أو V (P) ، فستكون متساوي الحرارة عبارة عن أشكال زائدة.
قوانين تشارلز وجاي لوساك
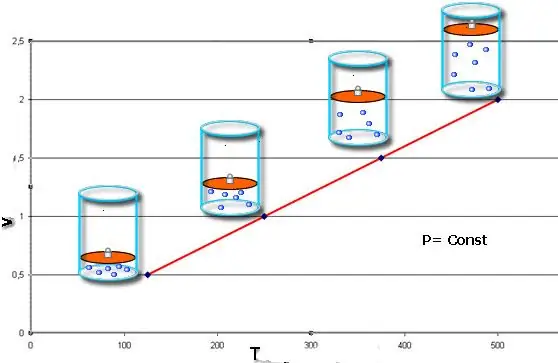
هذه القوانين تصف رياضيًا متساوي الضغط ومتساوي الضغطالعمليات ، أي مثل هذه التحولات بين حالات نظام الغاز ، حيث يتم الحفاظ على الضغط والحجم ، على التوالي. يمكن كتابة قانون تشارلز رياضياً على النحو التالي:
V / T=const عندما n ، P=const.
قانون جاي لوساك مكتوب على النحو التالي:
P / T=const عندما n ، V=const.
إذا تم تقديم كلا المساواة في شكل رسم بياني ، فسنحصل على خطوط مستقيمة تميل بزاوية ما على المحور x. يشير هذا النوع من الرسم البياني إلى تناسب مباشر بين الحجم ودرجة الحرارة عند ضغط ثابت وبين الضغط ودرجة الحرارة عند حجم ثابت.
لاحظ أن جميع قوانين الغاز الثلاثة المدروسة لا تأخذ في الاعتبار التركيب الكيميائي للغاز ، وكذلك التغيير في كمية المادة.
درجة الحرارة المطلقة
في الحياة اليومية ، اعتدنا على استخدام مقياس درجة الحرارة المئوية ، لأنه مناسب لوصف العمليات من حولنا. لذلك ، يغلي الماء عند 100oC ويتجمد عند 0oC. في الفيزياء ، تبين أن هذا المقياس غير مريح ، لذلك تم استخدام ما يسمى بمقياس درجة الحرارة المطلقة ، والذي قدمه اللورد كلفن في منتصف القرن التاسع عشر. وفقًا لهذا المقياس ، تُقاس درجة الحرارة بالكلفن (K).
يُعتقد أنه عند درجة حرارة -273 ، 15oC لا توجد اهتزازات حرارية للذرات والجزيئات ، تتوقف حركتها إلى الأمام تمامًا. تقابل درجة الحرارة هذه بالدرجات المئوية الصفر المطلق بالكلفن (0 كلفن). من هذا التعريفيتبع المعنى المادي لدرجة الحرارة المطلقة: إنها مقياس للطاقة الحركية للجسيمات التي تتكون منها المادة ، على سبيل المثال ، الذرات أو الجزيئات.
إلى جانب المعنى المادي أعلاه لدرجة الحرارة المطلقة ، هناك طرق أخرى لفهم هذه الكمية. واحد منهم هو قانون الغاز المذكور لتشارلز. لنكتبه بالصيغة التالية:
V1/ T1=V2/ T2=>
V1/ V2=T1/ T2.
تقول المساواة الأخيرة أنه عند كمية معينة من المادة في النظام (على سبيل المثال ، 1 مول) وضغط معين (على سبيل المثال ، 1 باسكال) ، يحدد حجم الغاز درجة الحرارة المطلقة بشكل فريد. بمعنى آخر ، الزيادة في حجم الغاز في ظل هذه الظروف ممكنة فقط بسبب زيادة درجة الحرارة ، ويشير الانخفاض في الحجم إلى انخفاض في قيمة T.
تذكر أنه على عكس درجة الحرارة المئوية ، لا يمكن أن تكون درجة الحرارة المطلقة سالبة.
مبدأ أفوجادرو ومخاليط الغاز
بالإضافة إلى قوانين الغاز المذكورة أعلاه ، تؤدي معادلة الحالة للغاز المثالي أيضًا إلى المبدأ الذي اكتشفه أميديو أفوجادرو في بداية القرن التاسع عشر ، والذي يحمل اسمه الأخير. ينص هذا المبدأ على أن حجم أي غاز عند ضغط ودرجة حرارة ثابتين يتم تحديده من خلال كمية المادة في النظام. تبدو الصيغة المقابلة كما يلي:
n / V=const عندما P ، T=const.
يؤدي التعبير المكتوب إلى قانون دالتون المعروف في فيزياء الغازات المثالية لمخاليط الغازات. هذهينص القانون على أن الضغط الجزئي للغاز في الخليط يتم تحديده بشكل فريد من خلال كسره الذري.
مثال على حل المشكلات
في وعاء مغلق بجدران صلبة تحتوي على غاز مثالي نتيجة التسخين ، زاد الضغط بمقدار 3 مرات. من الضروري تحديد درجة الحرارة النهائية للنظام إذا كانت قيمته الأولية 25oC.
أولاً ، لنحول درجة الحرارة من الدرجات المئوية إلى كلفن ، لدينا:
T=25 + 273 ، 15=298 ، 15 ك.
نظرًا لأن جدران الوعاء صلبة ، يمكن اعتبار عملية التسخين متساوية الصدأ. في هذه الحالة ، نطبق قانون Gay-Lussac ، لدينا:
P1/ T1=P2/ T2=>
T2=P2/ P1 T1.
وهكذا ، يتم تحديد درجة الحرارة النهائية من حاصل ضرب نسبة الضغط ودرجة الحرارة الأولية. باستبدال البيانات في المساواة ، نحصل على الإجابة: T2=894.45 K. درجة الحرارة هذه تتوافق مع 621.3oC.






