قاعدة Titius-Bode (تسمى أحيانًا ببساطة قانون Bode) هي الفرضية القائلة بأن الأجسام في بعض الأنظمة المدارية ، بما في ذلك الشمس ، تدور على طول أنصاف المحاور اعتمادًا على تسلسل الكواكب. تقترح الصيغة أنه ، بالامتداد إلى الخارج ، سيكون كل كوكب على بعد حوالي ضعف المسافة من الشمس مثل الكوكب السابق.
تنبأت الفرضية بشكل صحيح بمدارات سيريس (في حزام الكويكبات) وأورانوس ، لكنها فشلت في تحديد مدار نبتون واستبدلت في النهاية بنظرية تكوين النظام الشمسي. سميت على اسم يوهان دانيال تيتيوس ويوهان إيليرت بود.

أصول
يمكن العثور على أول إشارة لسلسلة تقترب من قانون بودي في David Gregory's Elements of Astronomy ، الذي نُشر عام 1715. يقول فيه: … بافتراض أن المسافة من الشمس إلى الأرض مقسمة إلى عشرة أجزاء متساوية ، ستكون مسافة منها حوالي أربعة ، من كوكب الزهرة سبعة ، من كوكب المريخ خمسة عشر ، عن كوكب المشتري اثنان وخمسون ومن زحل خمسة وتسعوناقتراح مشابه ، ربما مستوحى من غريغوري ، ظهر في عمل نشره كريستيان وولف عام 1724.
في عام 1764 ، قال تشارلز بونيه في كتابه تأمل الطبيعة: "نحن نعرف الكواكب السبعة عشر التي تشكل نظامنا الشمسي [أي الكواكب الرئيسية وأقمارها الصناعية] ، لكننا لسنا متأكدين من ذلك هم ليسوا أكثر ". لهذا ، في ترجمته عام 1766 لعمل Bonnet ، أضاف يوهان دانيال تيتيوس فقرتين خاصتين به في أسفل الصفحة 7 وأعلى الصفحة 8. لم يتم العثور على الفقرة الجديدة المحرف في النص الأصلي لبونيه: ولا في الإيطالية. ولا الترجمات الإنجليزية للعمل.
اكتشاف تيتيوس
هناك جزأين في النص المقحم لـ Titius. الأول يشرح تسلسل مسافات الكواكب من الشمس. يحتوي أيضًا على بضع كلمات حول المسافة من الشمس إلى المشتري. لكن هذه ليست نهاية النص.
يجدر قول بضع كلمات حول صيغة قاعدة Titius-Bode. انتبه للمسافات بين الكواكب واكتشف أن جميعها تقريبًا مفصولة عن بعضها البعض بنسبة تتوافق مع أحجام أجسامها. اقسم المسافة من الشمس إلى زحل على 100 جزء ؛ ثم يتم فصل عطارد بأربعة أجزاء من الشمس ؛ الزهرة - إلى 4 + 3=7 أجزاء من هذا القبيل ؛ الأرض - بمقدار 4 + 6=10 ؛ المريخ - بمقدار 4 + 12=16.
لكن لاحظ أنه من المريخ إلى المشتري هناك انحراف عن هذا التقدم الدقيق للغاية. يتبع كوكب المريخ مساحة 4 + 24=28 جزء من هذا القبيل ، ولكن حتى الآن لم يتم اكتشاف أي كوكب هناك. لكن هل يجب على اللورد المهندس أن يترك هذا المكان فارغًا؟ مطلقا. لذالنفترض أن هذا الفضاء ينتمي بلا شك إلى أقمار المريخ التي لم يتم اكتشافها بعد ، ونضيف أنه ربما لا يزال لدى المشتري بضعة أقمار صغيرة حوله لم يرها أي تلسكوب بعد.

صعود البود
في عام 1772 ، أكمل يوهان إليرت بود ، وهو في الخامسة والعشرين من عمره ، الإصدار الثاني من خلاصته الفلكية Anleitung zur Kenntniss des Gestirnten Himmels ("دليل معرفة السماء المرصعة بالنجوم") ، والتي أضاف الحاشية التالية ، في الأصل بدون مصدر ، لكن تمت الإشارة إليها في الإصدارات اللاحقة. في مذكرات Bode يمكن للمرء أن يجد إشارة إلى Titius مع الاعتراف الواضح بسلطته.

رأي بودي
هكذا تبدو قاعدة Titius-Bode في عرض الأخير: إذا كانت المسافة من الشمس إلى زحل تساوي 100 ، فسيتم فصل عطارد عن الشمس بأربعة أجزاء من هذا القبيل. الزهرة - 4 + 3=7. الأرض - 4 + 6=10. المريخ - 4 + 12=16.
الآن هناك فجوة في هذا التقدم المنظم. بعد كوكب المريخ ، هناك فضاء بحساب 4 + 24=28 ، حيث لم يُرَ كوكب واحد بعد. هل يمكننا أن نصدق أن مؤسس الكون ترك هذا الفضاء فارغًا؟ بالطبع لا. من هنا نصل إلى مسافة كوكب المشتري في شكل حساب 4 + 48=52 ، وأخيراً مسافة زحل - 4 + 96=100.

يبدو أن هاتين العبارتين بخصوص جميع الأنماط المحددة وأنصاف الأقطار المدارية تأتي من القديمالفلك. يعود العديد من هذه النظريات إلى ما قبل القرن السابع عشر.
التأثير
كان تيتيوس طالبًا للفيلسوف الألماني كريستيان فرايهر فون وولف (1679-1754). الجزء الثاني من النص المدرج في عمل Bonnet مبني على عمل فون وولف عام 1723 ، Vernünftige Gedanken von den Wirkungen der Natur.
يسند أدب القرن العشرين تأليف حكم تيتيوس-بود إلى فيلسوف ألماني. إذا كان الأمر كذلك ، يمكن أن يتعلم تيتيوس منه. كتب جيمس غريغوري مرجعًا قديمًا آخر في عام 1702 في كتابه Astronomiae Physicae et geometryae Elementa ، حيث أصبح تسلسل مسافات الكواكب 4 و 7 و 10 و 16 و 52 و 100 تطورًا هندسيًا للنسبة 2.
هذه هي الصيغة الأقرب لنيوتن ، وقد تم العثور عليها أيضًا في كتابات بنيامين مارتن وتوماس سيرد قبل سنوات من نشر كتاب بونيت في ألمانيا.
مزيد من العمل والآثار العملية
يأمل تيتيوس وبودي أن يؤدي القانون إلى اكتشاف كواكب جديدة ، وفي الواقع ، ساهم اكتشاف أورانوس وسيريس ، المسافة التي تتفق جيدًا مع القانون ، في قبوله من قبل العالم العلمي.
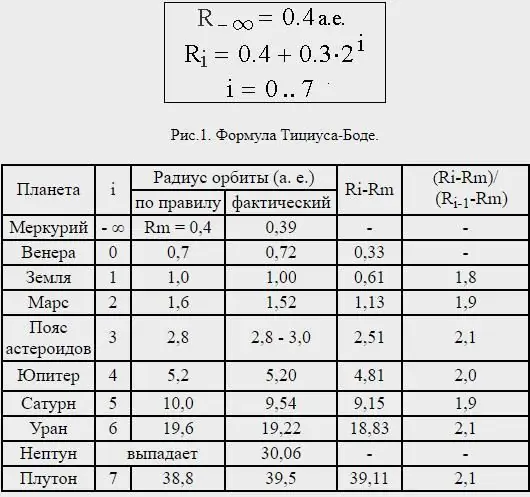
ومع ذلك ، كانت مسافة نبتون غير متسقة للغاية ، وفي الواقع ، بلوتو - الذي لا يعتبر الآن كوكبًا - يقع على مسافة متوسطة تتوافق تقريبًا مع قانون تيتيوس بود المتوقع للكوكب التالي خارج أورانوس.
القانون المنشور في الأصل كان مُرضيًا تقريبًا من قبل جميع الكواكب المعروفة - عطارد وزحل - مع وجود فجوة بينهماالرابع والخامس الكواكب. كان هذا يعتبر شخصية مثيرة للاهتمام ، ولكن ليست ذات أهمية كبيرة ، حتى اكتشاف أورانوس في عام 1781 ، والذي يتناسب مع السلسلة.
بناءً على هذا الاكتشاف ، دعا بود للبحث عن كوكب خامس. تم العثور على سيريس ، أكبر جسم في حزام الكويكبات ، في الموقع المتوقع لبود في عام 1801. تم قبول قانون Bode على نطاق واسع حتى تم اكتشاف Neptune في عام 1846 وتبين أنه غير متوافق مع القانون.
في نفس الوقت ، تم اكتشاف عدد كبير من الكويكبات في الحزام عبر سيريس خارج قائمة الكواكب. تمت مناقشة قانون بود من قبل عالم الفلك والمنطق تشارلز ساندرز بيرس في عام 1898 كمثال على التفكير الخاطئ.

تطور المشكلة
زاد اكتشاف بلوتو عام 1930 من تعقيد المشكلة. على الرغم من أنه لا يتطابق مع الموقف الذي تنبأ به قانون Bode ، إلا أنه كان متعلقًا بالموقف الذي تنبأ به القانون لنبتون. ومع ذلك ، فإن الاكتشاف اللاحق لحزام كايبر ، وعلى وجه الخصوص الكائن إيريس ، وهو أضخم من بلوتو ولكنه لا يتوافق مع قانون بودي ، أدى إلى زيادة مصداقية الصيغة.
مساهمة سيردا
قدم اليسوعي توماس سيردا دورة علم الفلك الشهيرة في برشلونة عام 1760 في الكرسي الملكي للرياضيات في كلية سانت جاومي دي كورديل (المدرسة الإمبراطورية والملكية لنبلاء كورديل). في تراتادو سيرداس ، تظهر مسافات الكواكب ، تم الحصول عليها من خلال تطبيق قانون كبلر الثالث ، بدقة 10-3.
إذا أخذنا مسافة 10 من الأرض والتقريب إلى عدد صحيح ، يمكن التعبير عن التقدم الهندسي [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2 ، من n=2 إلى n=8. وباستخدام حركة خيالية دائرية منتظمة لشذوذ كبلر ، يمكن الحصول على قيم Rn المقابلة لنسب كل كوكب على شكل rn=(Rn - R1) / (Rn-1 - R1) ، مما ينتج عنه 1.82 ؛ 1 ، 84 1 ، 86 ؛ 1.88 و 1.90 ، حيث rn=2 - 0.02 (12 - n) هي علاقة صريحة بين الاستمرارية Keplerian وقانون Titius-Bode ، والتي تعتبر مصادفة عددية عشوائية. نتيجة الحساب قريبة من اثنين ، ولكن يمكن اعتبار الشيطان بمثابة تقريب للرقم 1 ، 82.

متوسط سرعة الكوكب من n=1 إلى n=8 يقلل المسافة من الشمس ويختلف عن الانحدار المنتظم عند n=2 للتعافي من n=7 (الرنين المداري). هذا يؤثر على المسافة من الشمس إلى المشتري. ومع ذلك ، فإن المسافة بين جميع الكائنات الأخرى في إطار القاعدة سيئة السمعة التي خصصت لها المقالة يتم تحديدها أيضًا من خلال هذه الديناميكيات الرياضية.
الجانب النظري
لا يوجد تفسير نظري قوي يقوم عليه قاعدة Titius-Bode ، ولكن من الممكن أنه نظرًا لمزيج من الرنين المداري ونقص درجات الحرية ، فإن أي نظام كوكبي مستقر لديه احتمال كبير لتكرار النموذج الموصوف في هذه النظرية من قبل العالمين.
لأن هذا قد يكون مصادفة رياضية وليس "قانون الطبيعة" ، فإنه يطلق عليه أحيانًا قاعدة وليس "قانون". ومع ذلك ، يقول عالم الفيزياء الفلكية آلان بوس أن هذا الأمر ببساطةصدفة ، ولم تعد مجلة علوم الكواكب إيكاروس تقبل المقالات التي تحاول تقديم نسخ محسنة من "القانون".
الرنين المداري
يخلق الرنين المداري من الأجسام المدارية الرئيسية مناطق حول الشمس ليس لها مدارات مستقرة طويلة المدى. تدعم نتائج محاكاة تكوين الكوكب فكرة أن النظام الكوكبي المستقر المختار عشوائيًا من المرجح أن يفي بقاعدة Titius-Bode.

Dubrulle و Graner
أظهرDubrulle و Graner أن قواعد مسافة قانون القوة يمكن أن تكون نتيجة لنماذج السحب المنهارة لأنظمة الكواكب التي لها تماثلان: الثبات الدوراني (السحابة ومحتوياتها محورية) وثبات الحجم (السحابة و تبدو محتوياته متشابهة في جميع المقاييس).
هذا الأخير هو سمة من سمات العديد من الظواهر التي يعتقد أنها تلعب دورًا في تكوين الكواكب ، مثل الاضطرابات. المسافة من الشمس إلى كواكب النظام الشمسي ، التي اقترحها Titius و Bode ، لم يتم تعديلها في إطار دراسات Dubrulle و Graner.






