الغازات ، من وجهة نظر الديناميكا الحرارية ، موصوفة بمجموعة من الخصائص العيانية ، أهمها درجة الحرارة والضغط والحجم. يشير ثبات إحدى هذه المعلمات والتغيير في الاثنين الأخريين إلى حدوث عملية متساوية واحدة أو أخرى في الغاز. سنخصص هذه المقالة للإجابة التفصيلية للأسئلة القائلة بأن هذه عملية متساوية الصدمات ، وكيف تختلف عن التغيرات متساوي الحرارة ومتساوية الضغط في حالات نظام الغاز.
الغاز المثالي في الفيزياء

قبل الإجابة على السؤال القائل بأن هذه عملية متوازنة ، يجب أن تتعرف على مفهوم الغاز المثالي بشكل أفضل. في الفيزياء ، يُفهم على أنه أي غاز يتجاوز فيه متوسط الطاقة الحركية للجسيمات المكونة له بكثير الطاقة الكامنة لتفاعلها ، والمسافات بين هذه الجسيمات أكبر بعدة مرات من أبعادها الخطية. في ظل الظروف المذكورة ، من الممكن ، عند التنفيذلا تأخذ الحسابات في الاعتبار طاقة التفاعل بين الجسيمات (تساوي صفرًا) ، ويمكن أيضًا افتراض أن الجسيمات هي نقاط مادية لها كتلة معينة م.
العملية الوحيدة التي تحدث في الغاز المثالي هي اصطدام الجسيمات بجدران الوعاء الذي يحتوي على المادة. تتجلى هذه الاصطدامات في الممارسة العملية على أنها وجود ضغط معين في الغاز P.
كقاعدة عامة ، يمكن اعتبار أي مادة غازية تتكون من جزيئات خاملة كيميائيًا نسبيًا وذات ضغط منخفض ودرجات حرارة عالية غازًا مثاليًا بدقة كافية لإجراء حسابات عملية.
معادلة تصف الغاز المثالي
بالطبع ، نحن نتحدث عن القانون العالمي لكلابيرون مينديليف ، والذي يجب فهمه جيدًا لفهم أن هذه عملية متوازنة. إذن ، معادلة الحالة الشاملة لها الشكل التالي:
PV=nRT.
أي ناتج الضغط P وحجم الغاز V يساوي ناتج درجة الحرارة المطلقة T وكمية المادة في المولات n ، حيث R هو عامل التناسب. تمت كتابة المعادلة نفسها لأول مرة بواسطة Emile Clapeyron في عام 1834 ، وفي السبعينيات من القرن التاسع عشر ، استبدل D. Mendeleev فيها مجموعة من القيم الثابتة لثابت غاز عالمي واحد R (8.314 J / (molK)))
وفقًا لمعادلة Clapeyron-Mendeleev ، في نظام مغلق ، يظل عدد جزيئات الغاز ثابتًا ، لذلك لا يوجد سوى ثلاث معلمات مجهرية يمكن أن تتغير (T ، Pو الخامس). الحقيقة الأخيرة تكمن وراء فهم العمليات المتساوية المختلفة التي سيتم مناقشتها أدناه.
ما هي عملية isochoric؟
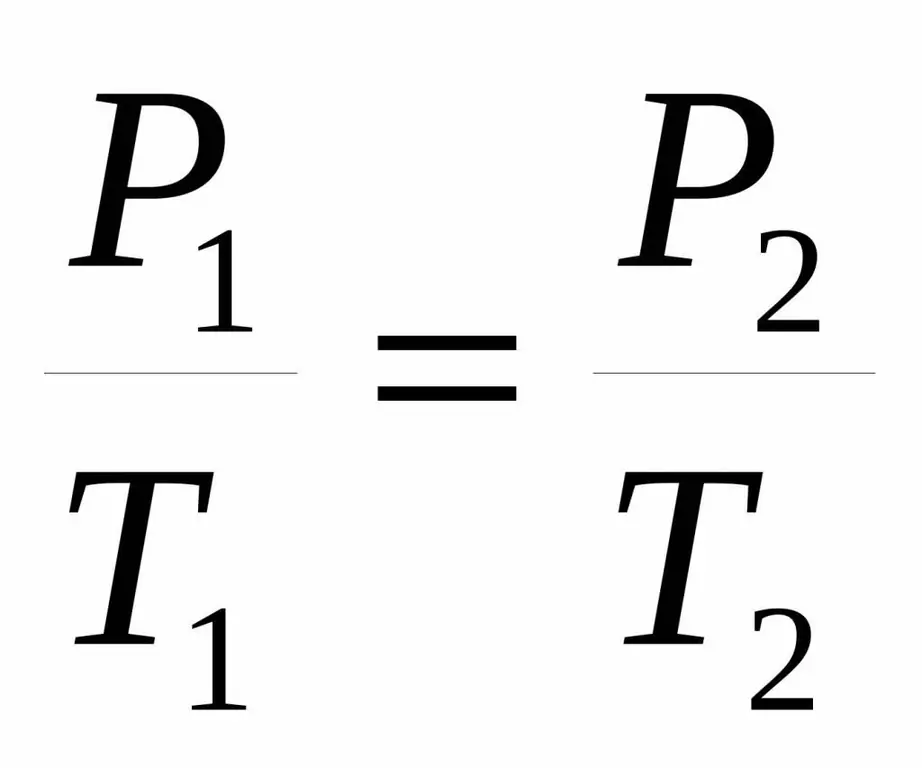
تُفهم هذه العملية على أنها أي تغيير على الإطلاق في حالة النظام ، حيث يتم الحفاظ على حجمه.
إذا لجأنا إلى معادلة الحالة العامة ، فيمكننا القول أنه في عملية متساوية الصدور فقط الضغط وتغير درجة الحرارة المطلقة في الغاز. لفهم بالضبط كيف تتغير المعلمات الديناميكية الحرارية ، نكتب التعبير الرياضي المقابل:
P / T=ثابت.
في بعض الأحيان يتم إعطاء هذه المساواة بصيغة مختلفة قليلاً:
P1/ T1=P2/ T2.
تسمى كلتا المساواة بقانون تشارلز على اسم عالم فرنسي حصل في نهاية القرن الثامن عشر على الاعتماد الملحوظ تجريبيًا.

إذا قمنا ببناء رسم بياني للوظيفة P (T) ، فإننا نحصل على اعتماد خط مستقيم ، وهو ما يسمى isochore. أي isochore (لجميع قيم n و V) هو خط مستقيم.
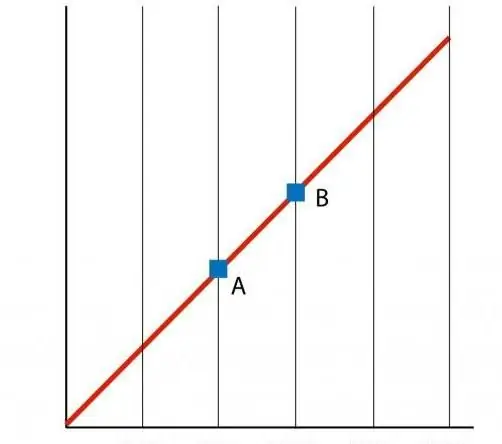
وصف الطاقة للعملية
كما لوحظ ، عملية متساوية الصدور هي تغيير في حالة النظام الذي يحدث في نظام مغلق ولكن ليس معزولًا. نحن نتحدث عن إمكانية التبادل الحراري بين الغاز والبيئة. بشكل عام ، أي إمداد للحرارة Q للنظام يؤدي إلى نتيجتين:
- يغير الطاقة الداخلية U ؛
- غازهل يعمل أ ، توسيع أو التعاقد.
الاستنتاج الأخير مكتوب رياضيًا على النحو التالي:
Q=U + A.
العملية المتساوية للغاز المثالي ، حسب تعريفها ، لا تعني العمل الذي يقوم به الغاز ، حيث يظل حجمه دون تغيير. هذا يعني أن كل الحرارة التي يتم توفيرها للنظام تذهب لزيادة طاقته الداخلية:
Q=U.
إذا قمنا باستبدال الصيغة الصريحة للطاقة الداخلية في هذا التعبير ، فيمكن تمثيل حرارة العملية متساوي الصدور على النحو التالي:
Q=z / 2nRT.
هنا z هو عدد درجات الحرية ، والتي تحددها الطبيعة متعددة الذرات للجزيئات التي يتكون منها الغاز. للغاز أحادي الذرة ، z=3 ، للغاز ثنائي الذرة - 5 ، وللغاز ثلاثي الذرات وأكثر - 6. هنا ، تحت درجات الحرية ، نعني الدرجات الانتقالية والدورانية.
إذا قارنا كفاءة تسخين نظام الغاز في عمليات متساوية الضغط ومتساوية الضغط ، ففي الحالة الأولى سنحصل على أقصى قدر من الكفاءة ، لأنه أثناء التغيير متساوي الضغط في حالة النظام ، يتمدد الغاز ، و يتم إنفاق جزء من المدخلات الحرارية على العمل.
عملية متساوية الضغط
أعلاه وصفنا بالتفصيل أن هذه عملية متوازنة. الآن دعنا نقول بضع كلمات عن العمليات المتماثلة الأخرى. لنبدأ مع متساوي الضغط. بناءً على الاسم ، يُفهم على أنه انتقال النظام بين الحالات عند ضغط مستمر. يصف قانون Gay-Lussac هذه العملية على النحو التالي:
V / T=ثابت.
كما هو الحال مع isochore ، يمثل متساوي القياس V (T) أيضًا خطًا مستقيمًا على الرسم البياني.
لمن أي عملية متساوية الضغط ، من الملائم حساب الشغل الذي يقوم به الغاز ، لأنه يساوي ناتج الضغط المستمر والتغير في الحجم.
عملية متساوية
هذه عملية تظل فيها درجة حرارة النظام ثابتة. يصفه قانون Boyle-Mariotte بأنه غاز مثالي. من الغريب أن نلاحظ أن هذا هو أول قانون غاز تم اكتشافه تجريبياً (النصف الثاني من القرن السابع عشر). يبدو تدوينها الرياضي كما يلي:
PV=ثابت.
تختلف العمليات Isochoric و isothermal من حيث التمثيل الرسومي ، لأن الوظيفة P (V) هي علاقة قطعية وليست علاقة خطية.
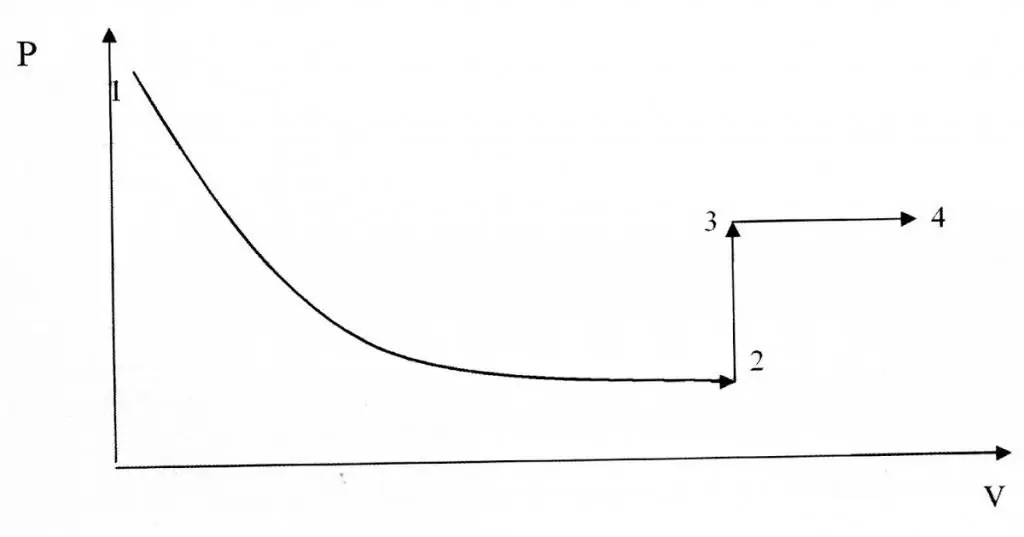
مثال على حل المشكلات
دعنا ندمج المعلومات النظرية الواردة في المقالة من خلال تطبيقها لحل مشكلة عملية. من المعروف أن النيتروجين الغازي النقي كان في أسطوانة عند ضغط 1 جو ودرجة حرارة 25 درجة مئوية. بعد تسخين أسطوانة الغاز وقياس الضغط فيها ، اتضح أن 1.5 ضغط جوي. ما هي درجة حرارة الغاز في الاسطوانة بعد التسخين؟ بأي كمية تغيرت الطاقة الداخلية للغاز إذا كان هناك 4 مولات من النيتروجين في البالون.
للإجابة على السؤال الأول نستخدم التعبير التالي:
P1/ T1=P2/ T2.
من حيث نحصل:
T2=P2/ P1 T1.
في هذا التعبير ، يمكن استبدال الضغط بوحدات عشوائيةقياسات ، لأنها تتقلص ، ودرجة الحرارة فقط في كلن. مع ذلك ، نحصل على:
T2=1.5 / 1298.15=447.224 ك
درجة الحرارة المحسوبة بالدرجات المئوية هي 174 درجة مئوية
نظرًا لأن جزيء النيتروجين ثنائي الذرة ، يمكن تحديد التغيير في طاقته الداخلية أثناء التسخين على النحو التالي:
ΔU=5/2nRΔT.
باستبدال القيم المعروفة في هذا التعبير ، سنحصل على إجابة السؤال الثاني من المشكلة: ΔU=+12.4 kJ.






