من بين الخصائص الرئيسية لخرائط المنطقة ، غالبًا ما يتم تمييز هذه الخريطة. هذه دقة الميزان. سنحلل في المقالة ما يخفيه هذا المفهوم في حد ذاته. سننظر أيضًا في ماهية المقياس بشكل عام ، وسنحدد أصنافه الرئيسية. دعنا نحلل كيف يرتبط مفهوم "الدقة الرسومية" بموضوع محادثتنا.
ما هذا؟
المقياس هو توضيح مهم يوضح مقدار كل سطر تم رسمه على الرسم أو الخطة أقل أو أكثر من الحجم الفعلي للكائن الذي يصوره. يتم تقديم هذه الإيضاحات في مستندات الرسم والخرائط رقميًا ورسميًا.
مقياس الخطط ودقة المقياس - مفاهيم يمكن العثور عليها في مجموعة متنوعة من المجالات:
- رسم الخرائط.
- تصميم
- الجيوديسيا.
- صورة
- النمذجة.
- البرمجة.
- الرياضيات.
- سينما
بعض هذه التطبيقات ، ميزاتها ، سننظر فيها في سياق المقال
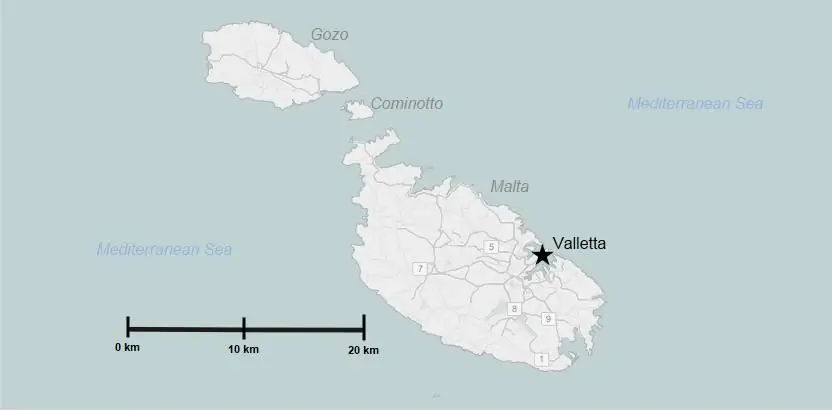
دقة القياس
والآنتعريف المفهوم الرئيسي. دقة المقياس - جزء من تباعد الأسطر الأفقي ، والذي يعني 0.1 مم على الرسم. لماذا تم اختيار هذه القيمة؟
0، 1 مم مقبولة هنا لكون هذا هو أصغر جزء يمكن تمييزه بالعين البشرية في الصورة دون استخدام معدات خاصة ، أدوات ، أجهزة.
لنأخذ مثالًا ملموسًا. معطى 1: 10000. ستكون دقة المقياس ، على التوالي ، 1 متر.لنحلل بمزيد من التفصيل:
- 1 سم على مخطط أو صورة هو 10000 سم (أو 100 م) على الأرض الحقيقية.
- 1 ملم في الصورة 1000 سم (أو 10 م)
- 0 ، 1 مم 100 سم (أو 1 م) على أرض حقيقية.
وبالتالي ، من السهل تحديد الدقة القصوى للمقياس. هذه هي المسافة من السطح الحقيقي ، والتي تساوي 0.1 مم على الخريطة - الحد الأدنى للجزء الذي يمكن للشخص أن يميزه.
دقة الرسم
والآن دعنا نتعرف على الدقة الرسومية للمقاييس. هذه ميزة أخرى مهمة عند استخدام الخطط والخرائط.
ترتبط دقة الجرافيك بدقة "و" العين البشرية. بدوره ، فإنه يجعل "G". ومن ثم G=u.
أي ، إذا كانت الزاوية "و" بين المتجهات في نقطتين "B" و "L" عند عرضها بواسطة مراقب بمستوى رؤية عادي هي "G" أو أكثر ، فسيتم إدراكها كنقطتين. إذا كانت هذه الزاوية لمفهوم الدقة أقل من "G" ، فسيرى الشخص "L" و "B" على أنهما واحدنقطة
من الأفضل التعرف على تعريف دقة المقياس في مثال محدد. لنفترض أن شخصًا ما قام بفحص الخريطة من أفضل مسافة "b" تساوي 35 سم ، قيمة G=u. أنت الآن بحاجة إلى تحديد أصغر مسافة (أي الدقة الرسومية) بين "B" و "L" ، والتي سيظل ينظر إليها من قبل المراقب كنقطتين مختلفتين. ها هي العملية الحسابية:
1 - هو! - 1/3438 × 350 ملم=0.1 ملم
1/3438 هي قيمة الزاوية u=r ، والتي يتم التعبير عنها في هذه الحالة بالراديان (3438 'هو عدد الدقائق بالراديان).
وبالتالي ، فإن قيمة الإخراج 0.1 مم هي الدقة الرسومية للخطة أو الخريطة.
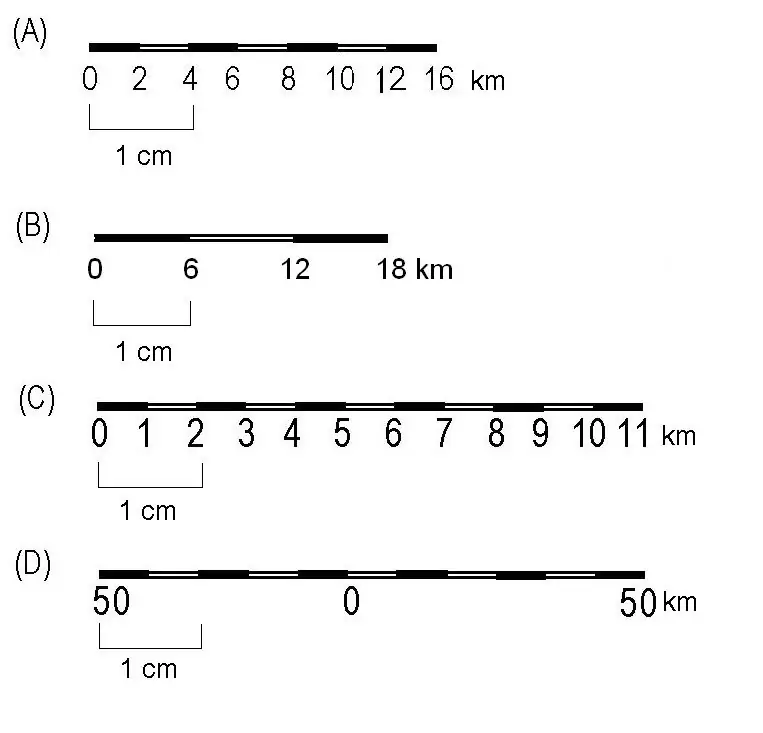
اتصال المفاهيم
الآن دعونا نرى كيف يرتبط المصطلح أعلاه بالمصطلح الرئيسي. دقة المقياس كما نتذكر هي المسافة على سطح الأرض والتي تساوي 0.1 مم على المستند.
يمكنك اشتقاق الصيغة:
T=جم=0.1 م مم.
فك عناصره:
- T - دقة المقياس
- M هو مقام المقياس.
- r=0.1 مم - دقة الرسم
من هنا يمكننا استنتاج التفسير ذي الصلة. دقة المقياس - دقة الرسوم البيانية ، والتي يتم التعبير عنها في مقياس الخريطة أو الخطة. وما هي النتيجة؟ ستصبح دقة الرسم ثابتة (0.1 مم) لجميع المقاييس الموجودة.
وفقًا لذلك ، ستتغير دقة المقياس معها. كلما كان ذلك أعلى ، كلما اختار المترجم المقياس أكبر.
والآنسنتعامل مع ميزات مثل هذه الخاصية مثل المقياس في مختلف مجالات التطبيق.
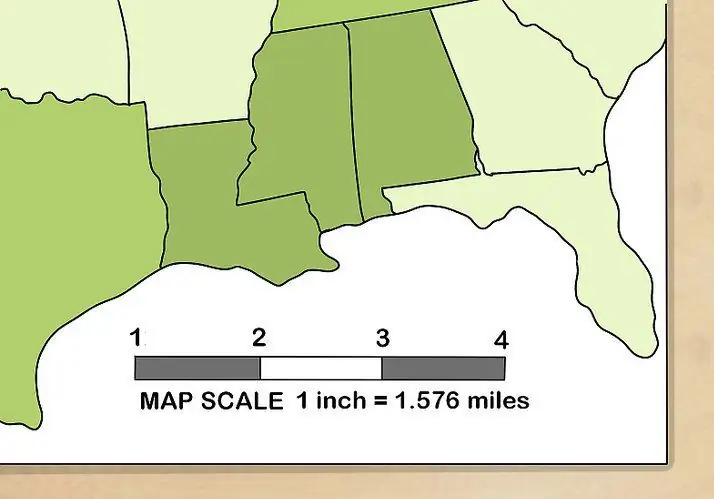
التصميم والجيوديسيا ورسم الخرائط
نعرف ما تعنيه دقة مقياس "500" - 1: 500. دعونا الآن نفكر في أنواعها النموذجية في مجال التصميم ورسم الخرائط والجيوديسيا:
- مقياس عددي. المؤشر مكتوب على شكل كسر. سيكون بسطه واحدًا ، وسيكون مقامه درجة من تقليل الإسقاط على الخريطة. على سبيل المثال ، لنأخذ مقياسًا من 1: 5000. فهذا يعني أن 1 سم على مخطط ، والخريطة 5000 سم (أو 50 مترًا) على أرض حقيقية. وفقًا لذلك ، سيكون هناك مقياس أكبر مقامه أصغر. إذن ، 1: 1000 ستكون أكبر من 1: 20000.
- مقياس مسمى. يحدد مترجم الخريطة في المستند المسافة على الأرض الحقيقية التي تساوي 1 سم على الخطة. إليك مثال: "هناك 1000 كيلومتر في 1 سنتيمتر". أو باختصار: "1 سم=100 كم".
- مقياس الرسم. في المقابل ، سيتم تقسيمها إلى عرضي وخطي. سنقوم بتحليلها بشكل منفصل.

مجموعة متنوعة من فئة الرسوم
ما هي دقة الميزان - المقياس العرضي؟ دعنا نتعرف على الخصائص:
- خطي. يتم تمثيل هذا المقياس الرسومي على الخريطة كمسطرة ، والتي سيتم تقسيمها إلى أجزاء حقيقية.
- عرضي. هذا مقياس رسومي يتم تمثيله كرسم رمزي.يعتمد بناؤها على تناسب أجزاء الخطوط المتوازية التي تتقاطع مع جوانب الزاوية. هذا المقياس قابل للتطبيق لقياس أكثر دقة لطول الخطوط على الخطط. يستخدمونها بهذه الطريقة: يقيسون الطول على الخط السفلي لمقياس عرضي معين بحيث يكون الطرف الأيمن على مسافة كاملة (OM) ، والطرف الأيسر أكبر من الصفر. إذا كانت الساق اليسرى في هذه الحالة هي بين الأقسام العاشرة ، على التوالي ، من الجزء الأيسر (من 0) ، ثم يقوم المتخصص برفع ساقي العداد لأعلى. حتى تكون الساق اليسرى من العداد بالفعل عند تقاطع أي خط أفقي وأي خط مستعرض. لكن يجب أن تكون الساق اليمنى أيضًا على هذا الخط الأفقي. الحد الأدنى للقرص المضغوط هنا هو 0.2 ملم. وفقًا لذلك ، أصغر دقة هي 0.1 مم.
سلسلة مقاييس الصورة في التصميم
نحن نعلم بالفعل ما تعنيه دقة المقياس 1: 500. لكن في أي الحالات يختارها المترجم؟ دعونا نحلل هذا السؤال:
- تصغير. وفقًا لذلك ، يتم استخدامها في الحالات التي يكون فيها من الضروري تصوير كائن على مخطط ، وهو تضاريس تتجاوزه بشكل كبير في المنطقة. إذا لجأ المترجم إلى تصميم المخططات الرئيسية ذات الأحجام الكبيرة بشكل خاص ، فسيحتاج إلى استخدام المقاييس التالية: 1: 2000 ، 1: 5000 ، 1: 10000 ، 1: 20000 ، 1: 25000 ، 1: 50000.
- الحجم الفعلي. إذا كنت تريد تصوير الكائن على الخطة "كما هو" ، فارجع إلى المقياس "واحد لواحد". وفقًا لذلك ، سيتوافق الطول الحقيقي 1 سم هنا مع 1 سم من الطول على الخطة.
- موازينالتكبير. ضروري في الحالات التي يكون فيها مطلوبًا لتصوير كائن صغير جدًا على الخطة للتعرف التفصيلي على مظهره ، الجهاز.
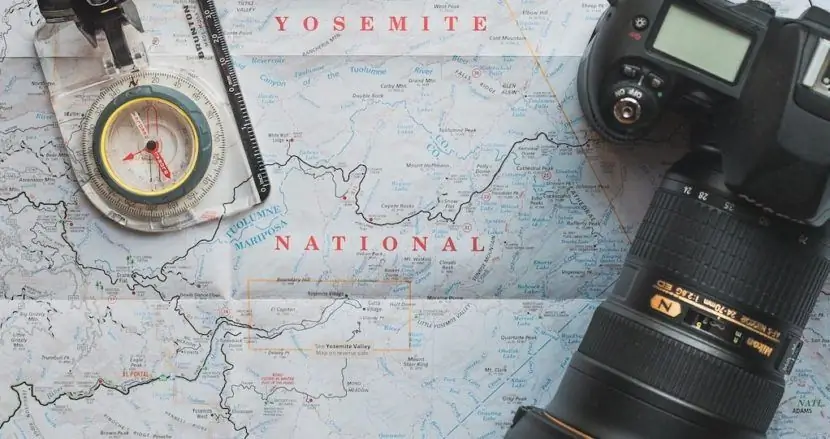
في الصورة
بالطبع ، 1: 10000 دقة مقياس أكثر ارتباطًا برسم الخرائط. لكن هذا ينطبق أيضًا على عالم التصوير. المقياس هنا يعني نسبة ما يسمى بالأبعاد الخطية للصورة التي تم الحصول عليها على مصفوفة فائقة الحساسية أو على فيلم فوتوغرافي إلى حجم إسقاط منطقة الإسقاط المقابلة على مستوى عمودي على الكاميرا.
هناك مصورون يقيسون المقياس كنسبة حجم كائن حقيقي إلى حجمه على شاشة أو ورق فوتوغرافي أو وسائط أخرى. لكن الطريقة الصحيحة لتحديد الحجم في الصورة تعتمد فقط على السياق الذي تستخدم فيه الصورة.
في التصوير الفوتوغرافي ، المقياس مهم أيضًا عند حساب عمق أي كائن تم تصويره بشكل حاد ، الفضاء. اليوم ، يتمتع المتخصصون بإمكانية الوصول إلى مجموعة واسعة جدًا من المقاييس من الحجم اللامتناهي (المستخدم عند تصوير الأجرام السماوية البعيدة) إلى الحجم الكبير جدًا (بدون استخدام المرفقات البصرية الخاصة ، على سبيل المثال ، اليوم من الممكن الحصول على صورة بمقياس 10: 1)
هنا ، يعتبر التصوير الفوتوغرافي المقرب بالفعل بمثابة تصوير بمقياس 1: 1 (وبالتالي ، أكبر). ولكن مع انتشار الكاميرات الرقمية صغيرة الحجم ، أصبح التصوير الفوتوغرافي المقرب أيضًا يُطلق عليه النمط عندما توضع العدسة على مسافة قريبة جدًا من الهدف. بالنظر إلى التعريف الكلاسيكي ، إذنمثل هذا التفسير لن يكون صحيحا.
في النمذجة
لكل نوع من نمذجة مقاعد البدلاء (أو مقياس) ، يتم تحديد المقاييس الخاصة به. وهي تتكون من عدة مقاييس تتميز بدرجة معينة من الاختزال. ومن المثير للاهتمام ، أنه لكل نوع من أنواع النمذجة (السكك الحديدية ، والسيارات ، ونمذجة السفن ، والمعدات العسكرية ، ونمذجة الطائرات) ، هناك بعض سلاسل المقاييس التي تم تشكيلها تاريخيًا والتي لا تتقاطع مع غيرها.
هنا يتم حساب المقياس بصيغة بسيطة:
L / M=X.
فك:
- L - المعلمات الأصلية.
- M - المقياس المطلوب للعمل.
- X هي القيمة المطلوبة.
في البرمجة
في هذا المجال ، سيكون المقياس الزمني المزعوم مهمًا. لنكتشف ما هو عليه
في نظام تشغيل مشاركة الوقت ، من المهم جدًا توفير "الوقت الفعلي" لمهام محددة. وهو يختلف في أن معالجة الأحداث الخارجية تمر دون تأخير أو ثغرات إضافية. هنا سيكون هناك مفهوم آخر مهم - "مقياس الوقت الحقيقي". لكن يجب أن يكون مفهوماً أنه لا علاقة مباشرة لها بالمقياس الموجود على الخرائط. هذا مجرد اصطلاح اصطلاحي.
في تكنولوجيا الأفلام
في تكنولوجيا الأفلام ، دقة المقياس الزمني مهمة أيضًا. يعني الأخير مؤشرًا كميًا لإبطاء أو تسريع الحركة ، والذي سيكون مساويًا لنسبة معدل إطار الإسقاط إلى معدل التصوير.
اعتبر هذا بعبارات بسيطةمثال. يبلغ معدل إطارات العرض لتصوير الفيلم 24 إطارًا في الثانية. تم التصوير في نفس الوقت "بسرعة" 72 لقطة / ثانية. سيكون المقياس الزمني في هذه الحالة هو 1: 3.
وماذا سيعني ، على سبيل المثال ، 2: 1؟ هذا أسرع مرتين من التدفق القياسي لما يحدث على الشاشة.
في الرياضيات
في هذه المنطقة ، يشير المقياس إلى العلاقة الخطية بين بعدين. أيضًا ، في العديد من المناطق القابلة للتطبيق عمليًا ، ستكون هذه هي نسبة حجم الصورة إلى الحجم الفعلي للصورة.
في الرياضيات ، المقياس هو نسبة أي مسافة على الخريطة إلى المسافة الحقيقية على الأرض الحقيقية. إذا نظرنا إلى المثال ، هذا هو نفسه كما في رسم الخرائط. لنفترض أن 1: 100.000.000 إذن ، 1 سم في الصورة هو 100.000 سم في الواقع. أي ألف متر أو كيلومتر واحد
المقياس خاصية قابلة للتطبيق على نطاق واسع. هذا عنصر أساسي ومتكامل في تطوير الخطط ورسومات الكائنات وخرائط المنطقة. يتم استخدامه في تصميم الجيوديسيا ورسم الخرائط ذات الصلة بالتصوير وتكنولوجيا الأفلام والبرمجة والرياضيات. هو نفسه يتميز بالدقة - نسبة المسافة الحقيقية إلى المسافة المقبولة على الخريطة.






