السعة الحرارية للغاز هي كمية الطاقة التي يمتصها الجسم عند تسخينه بدرجة واحدة. دعونا نحلل الخصائص الرئيسية لهذه الكمية المادية.

تعريفات
الحرارة النوعية للغاز هي وحدة كتلة مادة معينة. وحدات قياسه هي J / (kg · K). كمية الحرارة التي يمتصها الجسم في عملية تغيير حالته التراكمية لا ترتبط فقط بالحالة الأولية والنهائية ، ولكن أيضًا بطريقة الانتقال.

قسم
السعة الحرارية للغازات مقسومة على القيمة المحددة عند الحجم الثابت (Cv) ، الضغط المستمر (Cр).
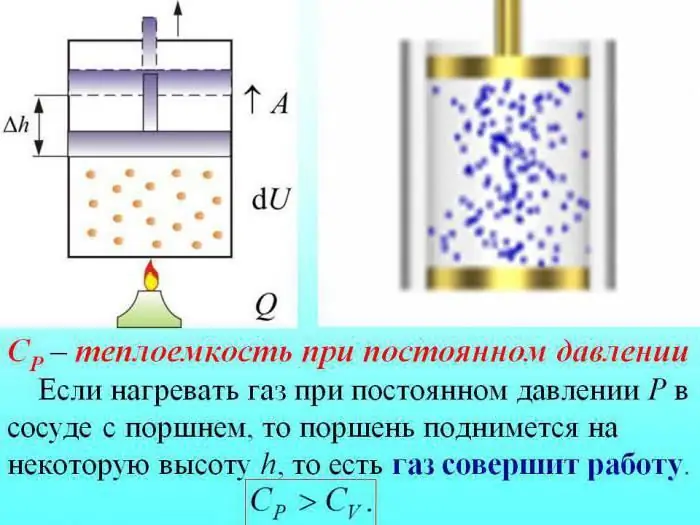
في حالة التسخين دون تغيير الضغط ، يتم إنفاق بعض الحرارة لإنتاج عمل تمدد الغاز ، ويتم إنفاق جزء من الطاقة لزيادة الطاقة الداخلية.
يتم تحديد السعة الحرارية للغازات عند ضغط ثابت بكمية الحرارة التي يتم إنفاقها على زيادة الطاقة الداخلية.
حالة الغاز: الميزات والوصف
يتم تحديد السعة الحرارية للغاز المثالي مع الأخذ في الاعتبار حقيقة أن Сp-Сv=R. تسمى الكمية الأخيرة بثابت الغاز العام. قيمته تقابل 8.314 J / (مول ك).
عند إجراء الحسابات النظرية للسعة الحرارية ، على سبيل المثال ، وصف العلاقة مع درجة الحرارة ، لا يكفي استخدام الطرق الديناميكية الحرارية فقط ، فمن المهم أن تتسلح بعناصر الفيزياء الثابتة.
تتضمن السعة الحرارية للغازات حساب متوسط قيمة طاقة الحركة الانتقالية لبعض الجزيئات. يتم تلخيص هذه الحركة من الحركة الدورانية والترجمة للجزيء ، وكذلك من الاهتزازات الداخلية للذرات.
في الفيزياء الساكنة ، توجد معلومات تفيد بأن لكل درجة من درجات حرية الحركة الدورانية والترجمة ، توجد كمية للغاز تساوي نصف ثابت الغاز العام.

حقائق مثيرة للاهتمام
يُفترض أن يكون لجسيم غاز أحادي الذرة ثلاث درجات انتقالية من الحرية ، وبالتالي فإن الحرارة النوعية للغاز لها ثلاث درجات انتقالية ودرجتين دوران ودرجة اهتزازية واحدة. يؤدي قانون توزيعها المنتظم إلى معادلة الحرارة النوعية عند حجم ثابت بـ R.
أثناء التجارب ، وجد أن السعة الحرارية للغاز ثنائي الذرة تتوافق مع القيمة R. يفسر هذا التناقض بين النظرية والتطبيق من خلال حقيقة أن السعة الحرارية للغاز المثالي مرتبطة بالكم. التأثيرات ، لذلك ، عند إجراء الحسابات ، من المهم استخدام الإحصائيات القائمة على الكمميكانيكا.
بناءً على أسس ميكانيكا الكم ، فإن أي نظام من الجسيمات تتأرجح أو تدور ، بما في ذلك جزيئات الغاز ، يحتوي فقط على بعض القيم المنفصلة للطاقة.
إذا كانت طاقة الحركة الحرارية في النظام غير كافية لإثارة التذبذبات بتردد معين ، فإن مثل هذه الحركات لا تساهم في السعة الحرارية الإجمالية للنظام.
نتيجة لذلك ، تصبح درجة معينة من الحرية "مجمدة" ، ومن المستحيل تطبيق قانون التقسيم عليها.
السعة الحرارية للغازات هي خاصية مهمة للحالة التي يعتمد عليها عمل النظام الديناميكي الحراري بأكمله.
درجة الحرارة التي يمكن عندها تطبيق قانون التقسيم على درجة الحرية الاهتزازية أو الدورانية تتميز بنظرية الكم ، وتربط ثابت بلانك مع ثابت بولتزمان.

غازات ثنائية الذرة
الفجوات بين مستويات الطاقة الدورانية لهذه الغازات هي عدد قليل من الدرجات. الاستثناء هو الهيدروجين ، حيث يتم تحديد درجة الحرارة بمئات الدرجات.
لهذا السبب يصعب وصف السعة الحرارية للغاز عند الضغط المستمر بقانون التوزيع المنتظم. في الإحصاء الكمي ، عند تحديد السعة الحرارية ، يؤخذ في الاعتبار أن الجزء الاهتزازي ، في حالة انخفاض درجة الحرارة ، ينخفض بسرعة ويصل إلى الصفر.
تشرح هذه الظاهرة حقيقة أنه في درجة حرارة الغرفة لا يوجد عملياً أي جزء اهتزازي من السعة الحراريةغاز ثنائي الذرة ، يتوافق مع الثابت R.
يتم تحديد السعة الحرارية للغاز عند حجم ثابت في حالة مؤشرات درجات الحرارة المنخفضة باستخدام إحصائيات الكم. يوجد مبدأ نيرنست ، والذي يسمى القانون الثالث للديناميكا الحرارية. بناءً على صيغته ، ستنخفض السعة الحرارية المولارية للغاز مع انخفاض درجة الحرارة ، وتميل إلى الصفر.

ملامح المواد الصلبة
إذا كان من الممكن تفسير السعة الحرارية لمزيج من الغازات باستخدام الإحصاء الكمي ، فبالنسبة للحالة الصلبة للتجميع ، تتميز الحركة الحرارية بتقلبات طفيفة في الجسيمات بالقرب من موضع التوازن.
لكل ذرة ثلاث درجات اهتزازية من الحرية ، لذلك ، وفقًا لقانون التقسيم المتساوي ، يمكن حساب السعة الحرارية المولية للمادة الصلبة على أنها 3nR ، حيث يمثل n عدد الذرات في الجزيء.
من الناحية العملية ، هذا الرقم هو الحد الذي تميل إليه السعة الحرارية للجسم الصلب عند درجات الحرارة العالية.
يمكن الحصول على الحد الأقصى في درجات الحرارة العادية لبعض العناصر ، بما في ذلك المعادن. بالنسبة إلى n=1 ، يتم استيفاء قانون Dulong و Petit ، ولكن بالنسبة للمواد المعقدة ، يصعب الوصول إلى هذا الحد. نظرًا لأنه لا يمكن الحصول على الحد في الواقع ، يحدث تحلل أو ذوبان المادة الصلبة.
تاريخ نظرية الكم
مؤسسا نظرية الكم هما أينشتاين وديباي في بداية القرن العشرين. وهو يقوم على تكميم الحركات التذبذبية للذرات في معينكريستال. في حالة مؤشرات درجات الحرارة المنخفضة ، يتضح أن السعة الحرارية للجسم الصلب تتناسب طرديًا مع القيمة المطلقة المأخوذة مكعبًا. سميت هذه العلاقة بقانون ديباي. كمعيار يجعل من الممكن التمييز بين مؤشرات درجات الحرارة المنخفضة والعالية ، يتم أخذ مقارنتها بدرجة حرارة ديباي.
يتم تحديد هذه القيمة من خلال طيف اهتزازات الذرة في الجسم ، وبالتالي فهي تعتمد بشكل جدي على ميزات هيكلها البلوري.
QD هي قيمة بها عدة مئات من K ، لكنها ، على سبيل المثال ، أعلى بكثير في الألماس.
تساهم إلكترونات التوصيل مساهمة كبيرة في السعة الحرارية للمعادن. لحسابها ، يتم استخدام إحصائيات Fermi الكمومية. الموصلية الإلكترونية لذرات المعادن تتناسب طرديا مع درجة الحرارة المطلقة. نظرًا لأنها قيمة تافهة ، يتم أخذها في الاعتبار فقط عند درجات حرارة تميل إلى الصفر المطلق.
طرق تحديد السعة الحرارية
الطريقة التجريبية الرئيسية هي قياس المسعرات. لإجراء حساب نظري للقدرة الحرارية ، يتم استخدام الديناميكا الحرارية الإحصائية. إنه صالح للغاز المثالي ، وكذلك للأجسام البلورية ، ويتم تنفيذه على أساس البيانات التجريبية حول بنية المادة.
تعتمد الطرق التجريبية لحساب السعة الحرارية للغاز المثالي على فكرة التركيب الكيميائي ، ومساهمة المجموعات الفردية من الذرات في Ср.
بالنسبة للسوائل ، تُستخدم أيضًا الطرق التي تعتمد على استخدام الديناميكا الحراريةالدورات التي تجعل من الممكن الانتقال من السعة الحرارية لغاز مثالي إلى سائل من خلال مشتق درجة حرارة المحتوى الحراري لعملية التبخر.
في حالة وجود حل ، لا يُسمح بحساب السعة الحرارية كوظيفة مضافة ، نظرًا لأن القيمة الزائدة للسعة الحرارية للحل مهمة بشكل أساسي.
لتقييمها ، نحتاج إلى نظرية الحلول الإحصائية الجزيئية. الأصعب هو تحديد السعة الحرارية للأنظمة غير المتجانسة في التحليل الديناميكي الحراري.

الخلاصة
تسمح لك دراسة السعة الحرارية بحساب توازن الطاقة للعمليات التي تحدث في المفاعلات الكيميائية ، وكذلك في أجهزة إنتاج المواد الكيميائية الأخرى. بالإضافة إلى ذلك ، هذه القيمة ضرورية لاختيار أفضل أنواع المبردات.
في الوقت الحاضر ، يعد التحديد التجريبي للسعة الحرارية للمواد لفترات مختلفة من درجات الحرارة - من القيم المنخفضة إلى القيم العالية - هو الخيار الرئيسي لتحديد الخصائص الديناميكية الحرارية للمادة. عند حساب إنتروبيا وانثالبي مادة ما ، يتم استخدام تكاملات السعة الحرارية. تتيح لك المعلومات حول السعة الحرارية للكواشف الكيميائية في نطاق درجة حرارة معينة حساب التأثير الحراري للعملية. تتيح المعلومات حول السعة الحرارية للحلول حساب معلماتها الديناميكية الحرارية عند أي قيم درجة حرارة ضمن الفاصل الزمني الذي تم تحليله.
على سبيل المثال ، يتميز السائل بإنفاق جزء من الحرارة لتغيير قيمة الطاقة الكامنةتفاعل الجزيئات. هذه القيمة تسمى السعة الحرارية "التكوين" ، وتستخدم لوصف الحلول.
من الصعب إجراء حسابات رياضية كاملة دون مراعاة الخصائص الديناميكية الحرارية للمادة ، وحالة تجميعها. هذا هو السبب في استخدام السوائل والغازات والمواد الصلبة ، مثل السعة الحرارية النوعية ، مما يجعل من الممكن توصيف معلمات الطاقة لمادة ما.






