في الديناميكا الحرارية ، عند دراسة التحولات من الحالة الأولية إلى الحالة النهائية للنظام ، من المهم معرفة التأثير الحراري للعملية. يرتبط مفهوم السعة الحرارية ارتباطًا وثيقًا بهذا التأثير. في هذه المقالة ، سننظر في مسألة ما هو المقصود بالسعة الحرارية المتساوية للغاز.
الغاز المثالي
الغاز المثالي هو الغاز الذي تعتبر جزيئاته نقاط مادية ، أي ليس لها أبعاد ، ولكن لها كتلة ، وتتكون كل الطاقة الداخلية فيها فقط من الطاقة الحركية لحركة الجزيئات والذرات.
أي غاز حقيقي من الناحية المثالية لن يرضي النموذج الموصوف أبدًا ، نظرًا لأن جزيئاته لا تزال لها بعض الأبعاد الخطية وتتفاعل مع بعضها البعض باستخدام روابط فان دير فالس الضعيفة أو روابط كيميائية من نوع آخر. ومع ذلك ، عند الضغط المنخفض ودرجات الحرارة المرتفعة ، تكون المسافات بين الجزيئات كبيرة ، وتتجاوز طاقتها الحركية الطاقة الكامنة بعشرات المرات. كل هذا يجعل من الممكن تطبيق النموذج المثالي للغازات الحقيقية بدرجة عالية من الدقة.
الطاقة الداخلية للغاز
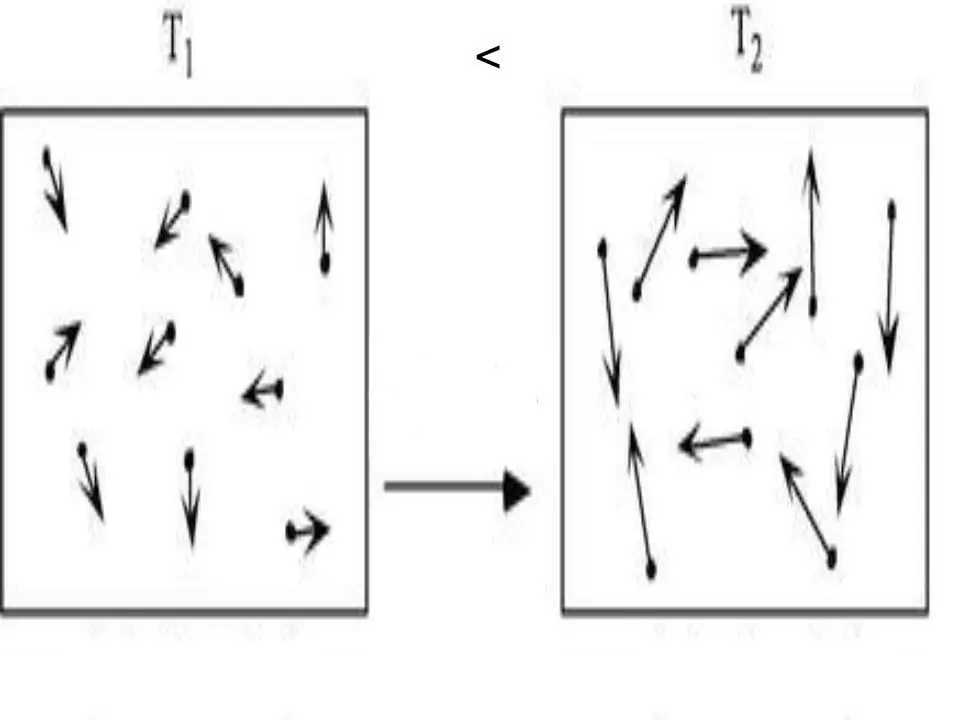
الطاقة الداخلية لأي نظام هي خاصية فيزيائية تساوي مجموع الطاقة الكامنة والحركية. نظرًا لأنه يمكن إهمال الطاقة الكامنة في الغازات المثالية ، يمكننا كتابة المساواة لها:
U=Eك.
حيث Ekهي طاقة النظام الحركي. باستخدام النظرية الحركية الجزيئية وتطبيق معادلة Clapeyron-Mendeleev العامة للحالة ، ليس من الصعب الحصول على تعبير لـ U. إنه مكتوب أدناه:
U=z / 2nRT.
هنا T و R و n هي درجة الحرارة المطلقة وثابت الغاز وكمية المادة على التوالي. قيمة z هي عدد صحيح يشير إلى عدد درجات الحرية التي يمتلكها جزيء الغاز.
السعة الحرارية متساوية الضغط ومتساوية الصدور
في الفيزياء ، السعة الحرارية هي كمية الحرارة التي يجب توفيرها للنظام قيد الدراسة لتسخينه بمقدار كلفن واحد. التعريف العكسي صحيح أيضًا ، أي السعة الحرارية هي مقدار الحرارة التي يطلقها النظام عند تبريده بمقدار كلفن واحد.
أسهل طريقة للنظام هي تحديد السعة الحرارية متساوية الصدور. يُفهم على أنه السعة الحرارية عند الحجم الثابت. نظرًا لأن النظام لا يؤدي العمل في ظل هذه الظروف ، يتم إنفاق كل الطاقة على زيادة احتياطيات الطاقة الداخلية. دعونا نشير إلى السعة الحرارية متساوية الصدور بالرمز CV، ثم يمكننا كتابة:
dU=CV dT.
أي التغيير في الطاقة الداخليةيتناسب بشكل مباشر مع التغير في درجة حرارته. إذا قارنا هذا التعبير بالمساواة المكتوبة في الفقرة السابقة ، فإننا نصل إلى صيغة CVفي غاز مثالي:
СV=z / 2nR.
هذه القيمة غير ملائمة للاستخدام في الممارسة العملية ، لأنها تعتمد على كمية المادة في النظام. لذلك ، تم تقديم مفهوم السعة الحرارية المتساوية المحددة ، أي القيمة التي يتم حسابها إما لكل 1 مول من الغاز أو لكل 1 كجم. دعونا نشير إلى القيمة الأولى بالرمز CV، الثانية - بالرمز CV م. بالنسبة لهم ، يمكنك كتابة الصيغ التالية:
CV=z / 2R ؛
CVm=z / 2R / M.
هنا M هي الكتلة المولية
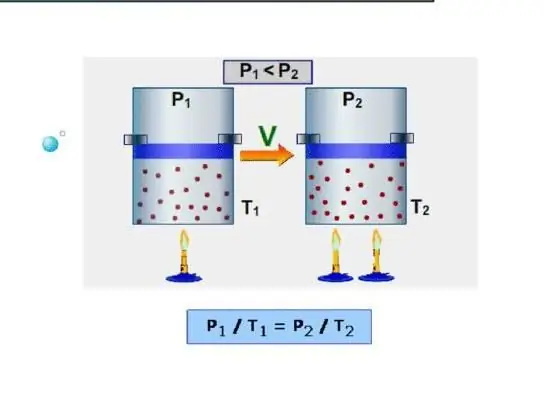
متساوي الضغط هو السعة الحرارية مع الحفاظ على ضغط ثابت في النظام. مثال على هذه العملية هو تمدد الغاز في أسطوانة تحت مكبس عند تسخينه. على عكس عملية متساوية الضغط ، أثناء عملية متساوي الضغط ، يتم إنفاق الحرارة المقدمة إلى النظام لزيادة الطاقة الداخلية وأداء العمل الميكانيكي ، أي:
H=dU + PdV.
المحتوى الحراري لعملية متساوية الضغط هو نتاج السعة الحرارية متساوية الضغط والتغير في درجة الحرارة في النظام ، أي:
H=CP dT.
إذا أخذنا في الاعتبار التمدد عند ضغط ثابت قدره 1 مول من الغاز ، فسيتم كتابة القانون الأول للديناميكا الحرارية على النحو التالي:
CP dT=CV dT + RdT.
يتم الحصول على المصطلح الأخير من المعادلةكلابيرون مندليف. من هذه المساواة تتبع العلاقة بين السعات الحرارية متساوية الضغط والمتساوية:
CP=CV+ R
بالنسبة للغاز المثالي ، فإن السعة الحرارية المولية المحددة عند ضغط ثابت تكون دائمًا أكبر من الخاصية المتوازنة المقابلة بواسطة R=8 ، 314 J / (molK).
درجات حرية الجزيئات والسعة الحرارية
دعنا نكتب مرة أخرى الصيغة الخاصة بسعة الحرارة متساوي الصدور المولية المحددة:
CV=z / 2R.
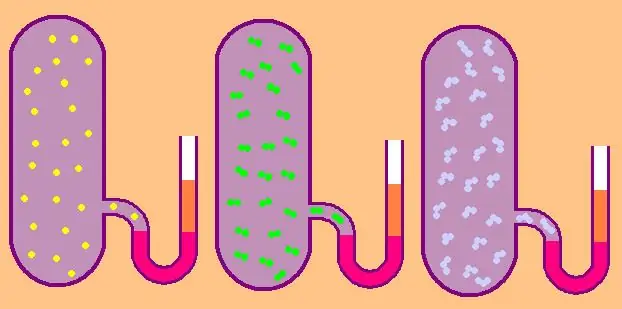
في حالة الغاز أحادي الذرة ، القيمة z=3 ، لأن الذرات في الفضاء لا يمكن أن تتحرك إلا في ثلاثة اتجاهات مستقلة.
إذا كنا نتحدث عن غاز يتكون من جزيئات ثنائية الذرة ، على سبيل المثال ، الأكسجين O2أو الهيدروجين H2، إذن ، بالإضافة إلى الحركة الانتقالية ، لا يزال بإمكان هذه الجزيئات الدوران حول محورين متعامدين بشكل متبادل ، أي أن z يساوي 5.
للجزيئات الأكثر تعقيدًا ، استخدم z=6.لتحديد CV






