عند مراجعة الأقران ، على سبيل المثال ، لتقييم القدرة التنافسية للمنتجات ، من الضروري ، كما هو الحال في أي عمل علمي ، إجراء معالجة البيانات الإحصائية. يبدأ الأخير بتحديد مدى اتساق آراء الخبراء ، والتعبير العددي عنها هو معامل التوافق.
لماذا نحتاج إلى تقييم إجماع خبير؟
هذا التقييم ضروري ، أولاً وقبل كل شيء ، لأن آراء الخبراء يمكن أن تختلف اختلافًا كبيرًا في المعايير المقدرة. في البداية ، يتم إجراء التقييم عن طريق ترتيب المؤشرات وتعيين معامل دلالة معين لها (الوزن). يؤدي الترتيب غير المتسق إلى عدم موثوقية هذه المعاملات إحصائيًا. يجب توزيع آراء الخبراء بعددهم المطلوب (أكثر من 7-10) حسب القانون العادي.
مفهوم معامل التوافق
هكذا. الاتساق هو التوافق. المعامل هو كمية بلا أبعاد توضح نسبة التشتت إلى أقصى تشتت في الحالة العامة. لنعمم هذه المفاهيم
معامل التوافق هو رقم من 0 إلى 1 ، يوضح تناسق آراء الخبراء عندماترتيب بعض الخصائص. كلما كانت هذه القيمة أقرب إلى 0 ، كلما انخفض التناسق. إذا كانت قيمة هذا المعامل أقل من 0.3 ، فإن آراء الخبراء تعتبر غير متسقة. عندما تكون قيمة المعامل في النطاق من 0.3 إلى 0.7 ، يعتبر الاتساق متوسطًا. تعتبر القيمة الأكبر من 0.7 درجة عالية من التناسق.
حالات الاستخدام
عند إجراء بحث إحصائي ، قد تنشأ مواقف لا يمكن فيها تمييز كائن من خلال تسلسلين ، يتم معالجتهما إحصائيًا باستخدام معامل التوافق ، ولكن من خلال عدة متواليات ، والتي يتم تصنيفها وفقًا لذلك من قبل خبراء من نفس المستوى من احتراف في مجال معين
يجب تحديد تناسق الترتيب الذي قام به الخبراء لتأكيد صحة الفرضية القائلة بأن الخبراء يقومون بقياسات دقيقة نسبيًا ، مما يسمح بتشكيل مجموعات مختلفة في مجموعات الخبراء ، والتي يتم تحديدها إلى حد كبير بواسطة العوامل البشرية ، في المقام الأول مثل الاختلافات في وجهات النظر ، والمفاهيم ، والمدارس العلمية المختلفة ، وطبيعة النشاط المهني ، وما إلى ذلك.
وصف موجز لطريقة الترتيب. مميزاته وعيوبه
عند الترتيب ، يتم استخدام طريقة الترتيب. يكمن جوهرها في حقيقة أن كل خاصية من سمات الكائن يتم تعيين مرتبة خاصة بها. علاوة على ذلك ، يتم تعيين هذه المرتبة لكل خبير مدرج في مجموعة الخبراءبشكل مستقل ، مما أدى إلى الحاجة إلى معالجة هذه البيانات من أجل تحديد توافق آراء الخبراء. تتم هذه العملية عن طريق حساب معامل التوافق.
الميزة الرئيسية لطريقة الترتيب هي سهولة تنفيذها
عيوب الطريقة الرئيسية هي:
- عدد صغير من كائنات الترتيب ، لأنه عندما يتجاوز عددها 15-20 ، يصبح من الصعب تعيين درجات تصنيف موضوعية ؛
- بناءً على استخدام هذه الطريقة ، يظل السؤال حول مدى بُعد الأشياء المدروسة عن بعضها البعض في الأهمية مفتوحًا.
عند استخدام هذه الطريقة ، يجب أن يؤخذ في الاعتبار أن التصنيفات تستند إلى نوع من النماذج الاحتمالية ، لذلك يجب تطبيقها بحذر ، بالنظر إلى النطاق.
معامل ترتيب توافق كيندال
يستخدم لتحديد العلاقة بين السمات الكمية والنوعية التي تميز الكائنات المتجانسة وترتيبها وفقًا لنفس المبدأ.
يتم تحديد هذا المعامل بالصيغة:
t=2S / (n (n-1)) ، حيث
S - مجموع الفروق بين عدد التسلسلات وعدد الانقلابات على السمة الثانية ؛
n - عدد المشاهدات

خوارزمية الحساب:
- يتم ترتيب قيم x بترتيب تصاعدي أو تنازلي.
- يتم ترتيب قيم y بالترتيب الذي تتوافق به مع قيم x
- لكل رتبة متتالية من y ، حدد عدد قيم الرتب الأعلى التي تليها. يتم جمعها ويتم حساب مقياس تطابق تسلسل الرتب في x و y.
- وبالمثل ، يتم حساب عدد مراتب y ذات القيم الأقل ، والتي يتم جمعها أيضًا.
- أضف عدد الرتب ذات القيم الأعلى وعدد الرتب ذات القيم الأقل ، مما ينتج عنه القيمة S.
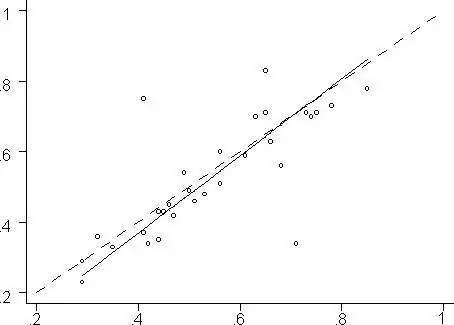
يوضح هذا المعامل العلاقة بين متغيرين ، وفي معظم الحالات يسمى معامل ارتباط رتبة كيندال. يمكن تمثيل هذا الاعتماد بيانيا.
تحديد المعامل
كيف يتم ذلك؟ إذا تجاوز عدد الميزات أو العوامل المرتبة 2 ، فسيتم استخدام معامل التوافق ، والذي ، في جوهره ، هو متغير متعدد من ارتباط الرتبة.
كن حذرا. يعتمد حساب معامل التوافق على نسبة انحراف مجموع مربعات الرتب من متوسط مجموع مربعات الرتب ، مضروبًا في 12 ، إلى مربع الخبراء ، مضروبًا في الفرق بين مكعب العدد من الأشياء وعدد الأشياء.
خوارزمية الحساب
لفهم من أين يأتي الرقم 12 في بسط صيغة الحساب ، فلنلقِ نظرة على خوارزمية التحديد.
لكل سطر برتب خبير معين ، يتم حساب مجموع الرتب ، وهي قيمة عشوائية.
يُعرّف معامل التوافق عمومًا على أنه نسبة تقدير التباين (D) إلى القيمة القصوى لتقدير التباين(Dmax). فلنقم بصياغة تعريفات هذه الكميات تباعا.
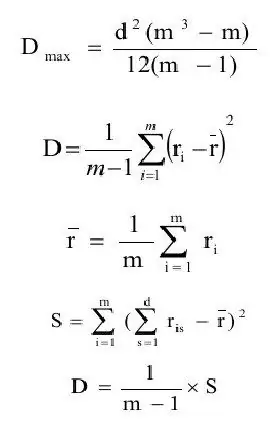
حيث ravg- تقدير التوقعات ؛
م - عدد الأشياء.
استبدال الصيغ الناتجة فيما يتعلق D بـ Dmaxنحصل على الصيغة النهائية لمعامل التوافق:
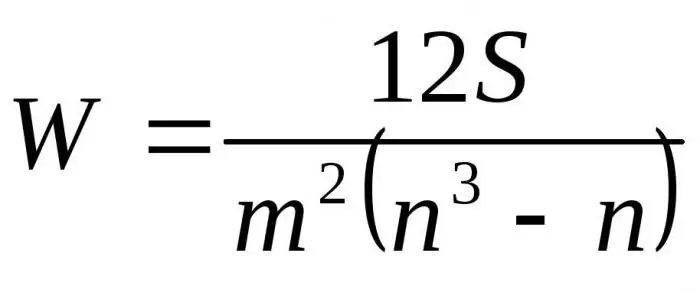
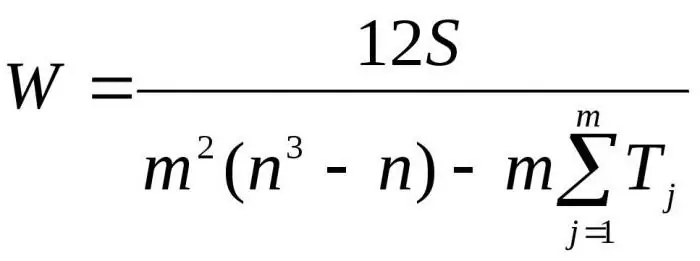
هنا م هو عدد الخبراء ، ن هو عدد الأشياء.
يتم استخدام الصيغة الأولى لتحديد عامل التوافق إذا لم تكن هناك رتب ذات صلة. يتم استخدام الصيغة الثانية إذا كانت هناك رتب ذات صلة.
إذن ، انتهى حساب معامل التوافق. ماذا بعد؟ يتم تقييم القيمة التي تم الحصول عليها من حيث الأهمية باستخدام معامل بيرسون بضرب هذا المعامل في عدد الخبراء وعدد درجات الحرية (م -1). تتم مقارنة المعيار الناتج مع قيمة الجدول ، وإذا تجاوزت قيمة الأول الأخير ، فإنهم يتحدثون عن أهمية المعامل قيد الدراسة.
في حالة الرتب ذات الصلة ، يصبح حساب معيار بيرسون أكثر تعقيدًا إلى حد ما ويتم إجراؤه بواسطة النسبة التالية: (12S) / (d (m2+ م) - (1 / (م -1)) × (Ts1+ Ts2+ Tsn)
مثال
افترض أن طريقة الخبير تقيم القدرة التنافسية للزبدة المباعة في شبكة البيع بالتجزئة. دعونا نعطي مثالاً لحساب معامل التوافق. قبل تقييم القدرة التنافسية ، من الضروري تصنيف المستهلكخصائص هذا المنتج التي يتم تضمينها في التقييم. لنفترض أن هذه الخصائص ستكون كالتالي: الطعم والرائحة ، التناسق والمظهر ، اللون ، التعبئة والتغليف ووضع العلامات ، محتوى الدهون ، الاسم التجاري ، الشركة المصنعة ، السعر.
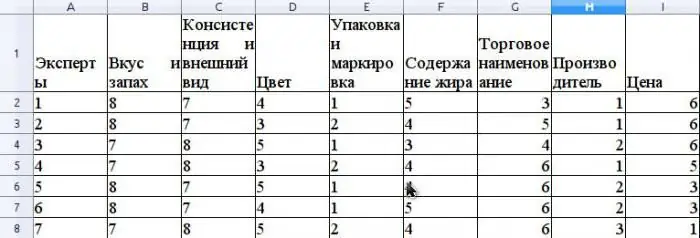
افترض أن فريق الخبراء يتكون من 7 خبراء. يوضح الشكل نتائج ترتيب هذه الخصائص.
يتم حساب متوسط قيمة r كمتوسط حسابي وسيكون 31.5. للعثور على S ، اجمع الفروق التربيعية بين rهوومتوسط r ، وفقًا للصيغة أعلاه ، وتحديد أن قيمة S هي 1718.
احسب معامل التوافق باستخدام الصيغة دون استخدام الرتب ذات الصلة (ستكون الرتب مرتبطة إذا كان لدى المستشار الخبير نفسه نفس الرتب لخصائص مختلفة).
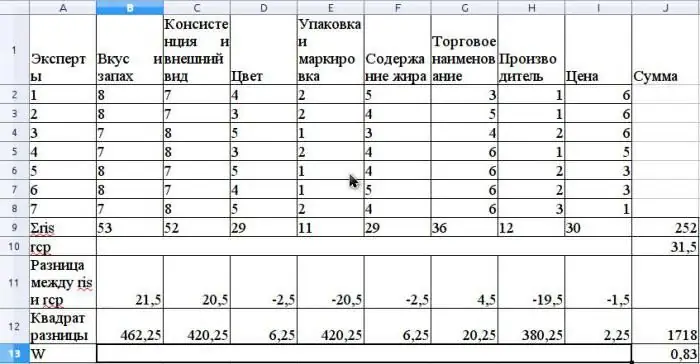
قيمة هذا المعامل ستكون 0.83 ، وهذا يدل على وجود إجماع قوي بين الخبراء.
تحقق من أهميتها باستخدام اختبار بيرسون:
7 × 0.83 × (8-1)=40.7.
اختبار جدول بيرسون عند مستوى أهمية 1٪ هو 18.5 ، وعند 5٪ - 14.1.
يوضح المثال بساطة الحساب وإمكانية الوصول إليه لأي شخص يعرف أساسيات الحسابات الرياضية. للتخفيف من حدتها ،استخدم نماذج جداول البيانات.
في الختام
هكذا يظهر معامل التوافق تناسق آراء العديد من الخبراء. كلما كانت المسافة أبعد من 0 وأقرب إلى 1 ، كانت الآراء أكثر اتساقًا. يجب تأكيد هذه المعاملات من خلال حساب معيار بيرسون.






